
【题目】如图,在平面直角坐标系中,Rt△ABC三个顶点都在格点上,点A、B.C的坐标分别为A(-1,3),B(-3,1),C(-1,1).请解答下列问题:
(1)画出△ABC关于y轴对称的△A1B1C1,并写出B1的坐标;
(2)画出△A1B1C1绕点C1顺时针旋转90°后得到的△A2B2C2;
(3)求出点A1走过的路径长.
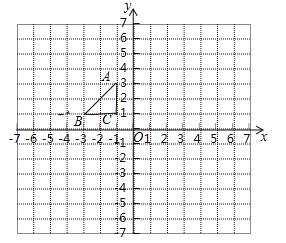
科目:初中数学 来源: 题型:
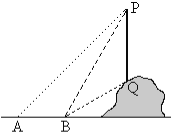
【题目】如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度.他们采取的方法是:先在地面上的点A处测得杆顶端点P的仰角是45°,再向前走到B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°,这时只需要测出AB的长度就能通过计算求出电线杆PQ的高度.你同意他们的测量方案吗?若同意,画出计算时的图形,简要写出计算的思路,不用求出具体值;若不同意,提出你的测量方案,并简要写出计算思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抽屉里放有4只白袜子和2只黑袜子.
(1)从中任意摸出1只袜子,记下颜色后放回,搅匀,再摸出1只袜子,摸出的两只袜子颜色相同的概率是多少.
(2)若第一次摸出不放回,摸出的两只袜子颜色相同的概率是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
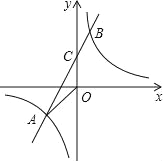
【题目】如图,已知A(n,﹣2),B(1,4)是一次函数y=kx+b的图象与反比例函数y=![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的解析式;
(2)求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果M个不同的正整数,对其中的任意两个数,这两个数的积能被这两个数的和整除,则称这组数为M个数的自然数组,如(3,6)为两个数的自然数组,因为(3×6)能被(3+6)整除;又如(15,30,60)为三个数的自然数组,因为(15×30)能被(15+30)整除,(15×60)能被(15+60)整除,(30×60)能被(30+60)整除…
(1)求证:2n和n(n﹣2)(n≥3,n为整数)组成的数组是两个数的自然数组;
(2)若(4a,5a,6a)是三个数的自然数组,求满足条件的三位正整数a,并判断(4a+5,5a+5,6a+5)是否为自然数组.
查看答案和解析>>
科目:初中数学 来源: 题型:
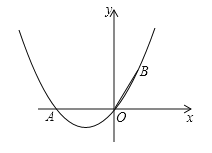
【题目】如图,在直角坐标系中,点A的坐标为(-2,0),OB=OA,且∠AOB=120°.
(1)求经过A、O、B三点的抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点C,使△OBC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;
(3)若点M为抛物线上一点,点N为对称轴上一点,是否存在点M、N使得A、O、M、N构成的四边形是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线 y=ax2﹣5ax+c 交 x 轴于点 A,点 A 的坐标为(4,0).
(1)用含 a 的代数式表示 c.
(2)当 a=![]() 时,求 x 为何值时 y 取得最小值,并求出 y 的最小值.
时,求 x 为何值时 y 取得最小值,并求出 y 的最小值.
(3)当 a=![]() 时,求 0≤x≤6 时 y 的取值范围.
时,求 0≤x≤6 时 y 的取值范围.
(4)已知点 B 的坐标为(0,3),当抛物线的顶点落在△AOB 外接圆内部时,直接写出 a的取值范围.
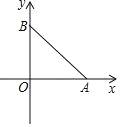
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司要把3000吨货物从M市运到W市.(每日的运输量为固定值)
(1)从运输开始,每天运输的货物吨数y(单位:吨)与运输时间x(单位:天)之间有怎样的函数关系式?
(2)因受到沿线道路改扩建工程影响,实际每天的运输量比原计划少20%,以致推迟1天完成运输任务,求原计划完成运输任务的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
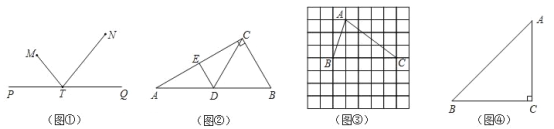
【题目】如图①,直线PQ同侧有两点M,N,点T在直线PQ上,若∠MTP=∠NTQ,则称点T为M,N在直线PQ上的投射点.
(1)如图②,在Rt△ABC中,∠B=60°,D为斜边AB的中点,E为AC的中点.求证:点D为C,E在直线AB上的投射点;
(2)如图③,在正方形网格中,已知点A,B,C三点均在格点上,请仅用没有刻度的直尺在AC上画出点P,在BC上画出点Q,使A,P在BC上的投射点Q满足CQ=2BQ;
(3)如图④,在Rt△ABC中,∠C=90°,AC=BC,在AB,BC边上是否分别存在点D,E,使点D为E,C在AB上的投射点,点E为A,D在BC上的投射点?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com