
【题目】已知α是锐角,且点A(![]() ,a),B(sinα+cosα,b), C(-m2+2m-2,c)都在二次函数y=-x2+x+3的图象上,那么a、b、c的大小关系是 ()
,a),B(sinα+cosα,b), C(-m2+2m-2,c)都在二次函数y=-x2+x+3的图象上,那么a、b、c的大小关系是 ()
A. a<b<c B. a<c<b C. b<c<a D. c<b<a
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
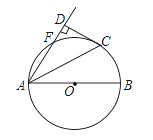
【题目】如图,AB是⊙O的直径,点F、C在⊙O上且![]() , 连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
, 连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
(1)求证:CD是⊙O的切线;
(2)若![]() , CD=4,求⊙O的半径.
, CD=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
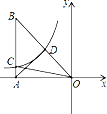
【题目】如图,已知反比函数![]() 的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于C,连结AD、OC,若△ABO的周长为
的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于C,连结AD、OC,若△ABO的周长为![]() ,AD=2,则△ACO的面积为( )
,AD=2,则△ACO的面积为( )
A. ![]() B. 1 C. 2 D. 4
B. 1 C. 2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们把横、纵坐标均为整数的点叫做整点.已知反比例函数y=![]() (m<0)与y=x2﹣4在第四象限内围成的封闭图形(包括边界)内的整点的个数为2,则实数m的取值范围为__.
(m<0)与y=x2﹣4在第四象限内围成的封闭图形(包括边界)内的整点的个数为2,则实数m的取值范围为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
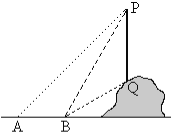
【题目】如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度.他们采取的方法是:先在地面上的点A处测得杆顶端点P的仰角是45°,再向前走到B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°,这时只需要测出AB的长度就能通过计算求出电线杆PQ的高度.你同意他们的测量方案吗?若同意,画出计算时的图形,简要写出计算的思路,不用求出具体值;若不同意,提出你的测量方案,并简要写出计算思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,小明随父母到某旅游胜地参观游览,他在游客中心O处测得景点A在其北偏东72°方向,测得景点B在其南偏东40°方向.小明从游客中心走了2千米到达景点A,已知景点B正好位于景点A的正南方向,求景点A与B之间的距离.(结果精确到0.1千米)
(参考数据:sin72°≈0.95,cos72°≈0.31,sin40°≈0.64,tan40°≈0.84)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】吴京同学根据学习函数的经验,对一个新函数![]() 的图象和性质进行了如下探究,请帮他把探究过程补充完整.
的图象和性质进行了如下探究,请帮他把探究过程补充完整.
(1)该函数的自变量![]() 的取值范围是______.
的取值范围是______.
(2)列表:
| … |
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| … |
|
|
|
|
|
|
|
|
| … |
表中![]() ________,
________,![]() _______.
_______.
(3)描点、连线
在下面的格点图中,建立适当的平面直角坐标系![]() 中,描出上表中各对对应值为坐标的点(其中
中,描出上表中各对对应值为坐标的点(其中![]() 为横坐标,
为横坐标,![]() 为纵坐标),并根据描出的点画出该函数的图象:
为纵坐标),并根据描出的点画出该函数的图象:

(4)观察所画出的函数图象,写出该函数的两条性质:
①_______________________________________;
②_______________________________________.
(5)函数![]() 与直线
与直线![]() 的交点有2个,那么
的交点有2个,那么![]() 的取值范围_________.
的取值范围_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
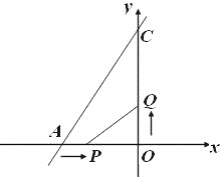
【题目】如图,已知,在直角坐标系xOy中,直线 y=![]() x+8与x轴、y轴分别交于点A、C,点P从A点开始以1个单位/秒的速度沿x轴向右移动,点Q从O点开始以2个单位/秒的速度沿y轴向上移动,如果P、Q两点同时出发,经过几秒钟,能使△PQO的面积为8个平方单位.com
x+8与x轴、y轴分别交于点A、C,点P从A点开始以1个单位/秒的速度沿x轴向右移动,点Q从O点开始以2个单位/秒的速度沿y轴向上移动,如果P、Q两点同时出发,经过几秒钟,能使△PQO的面积为8个平方单位.com
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A的坐标为(-2,0),OB=OA,且∠AOB=120°.
(1)求经过A、O、B三点的抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点C,使△OBC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;
(3)若点M为抛物线上一点,点N为对称轴上一点,是否存在点M、N使得A、O、M、N构成的四边形是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com