
【题目】吴京同学根据学习函数的经验,对一个新函数![]() 的图象和性质进行了如下探究,请帮他把探究过程补充完整.
的图象和性质进行了如下探究,请帮他把探究过程补充完整.
(1)该函数的自变量![]() 的取值范围是______.
的取值范围是______.
(2)列表:
| … |
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| … |
|
|
|
|
|
|
|
|
| … |
表中![]() ________,
________,![]() _______.
_______.
(3)描点、连线
在下面的格点图中,建立适当的平面直角坐标系![]() 中,描出上表中各对对应值为坐标的点(其中
中,描出上表中各对对应值为坐标的点(其中![]() 为横坐标,
为横坐标,![]() 为纵坐标),并根据描出的点画出该函数的图象:
为纵坐标),并根据描出的点画出该函数的图象:

(4)观察所画出的函数图象,写出该函数的两条性质:
①_______________________________________;
②_______________________________________.
(5)函数![]() 与直线
与直线![]() 的交点有2个,那么
的交点有2个,那么![]() 的取值范围_________.
的取值范围_________.
【答案】(1)一切实数;(2)![]() ;
;![]() ;(3)见解析;(4)①该函数有最小值没有最大值;②该函数图象关于直线x=2对称;(5)-5<m<0
;(3)见解析;(4)①该函数有最小值没有最大值;②该函数图象关于直线x=2对称;(5)-5<m<0
【解析】
(1)根据分式的分母不等于零,即可求解;
(2)把自变量的值代入即可求解;
(3)根据题意描点、连线即可该函数的图象;
(4)观察图象即可得出该函数的两条性质.
(5)根据函数![]() 与直线
与直线![]() 的交点有2个,可得方程
的交点有2个,可得方程![]() 有两个不相等的实数根,利用根的判别式即可求解,也可根据图像解答.
有两个不相等的实数根,利用根的判别式即可求解,也可根据图像解答.
解:(1)由![]() 知,x2-4x+5=
知,x2-4x+5=![]() ≠0,所以变量x的取值范围是一切实数.
≠0,所以变量x的取值范围是一切实数.
故答案为:一切实数;
(2)m= ![]() =
=![]() ,n=
,n=![]() =
=![]() ,
,
故答案为:![]() ;
;![]() ;
;
(3)建立适当的直角坐标系,描点画出图形,如下图所示: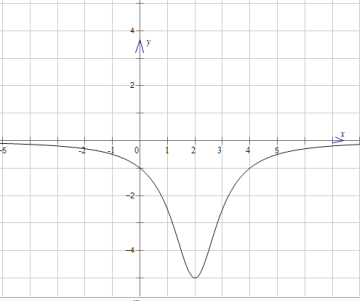
(4)观察所画出的函数图象,有如下性质:
①该函数有最小值没有最大值;
②该函数图象关于直线x=2对称.
故答案为:该函数有最小值没有最大值;该函数图象关于直线x=2对称;
(5)∵函数![]() 与直线
与直线![]() 的交点有2个,
的交点有2个,
∴方程![]() 有两个不相等的实数根,整理方程得:
有两个不相等的实数根,整理方程得:![]()
∴![]() ,即
,即![]() ,解得-5<m<0,
,解得-5<m<0,
∴![]() 的取值范围为:-5<m<0.
的取值范围为:-5<m<0.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商家经销一种绿茶,用于装修门面已投资3000元.已知绿茶每千克成本50元,经研究发现销量y(kg)随销售单价x(元/kg)的变化而变化,具体变化规律如表所示:
销售单价x(元/kg) | … | 70 | 75 | 80 | 85 | 90 | … |
月销售量y(kg) | … | 100 | 90 | 80 | 70 | 60 | … |
设该绿茶的月销售利润为w(元)(销售利润=单价×销售量﹣成本)
(1)请根据上表,写出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求w与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,w的值最大?
(3)若在第一个月里,按使w获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于80元,要想在全部收回装修投资的基础上使第二个月的利润至少达到1700元,那么第二个月时里应该确定销售单价在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
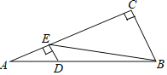
【题目】如图,在△ABC中,∠C=90°,∠A=30°,D为AB上一点,且AD:DB=1:3,DE⊥AC于点E,连接BE,则tan∠CBE的值等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知α是锐角,且点A(![]() ,a),B(sinα+cosα,b), C(-m2+2m-2,c)都在二次函数y=-x2+x+3的图象上,那么a、b、c的大小关系是 ()
,a),B(sinα+cosα,b), C(-m2+2m-2,c)都在二次函数y=-x2+x+3的图象上,那么a、b、c的大小关系是 ()
A. a<b<c B. a<c<b C. b<c<a D. c<b<a
查看答案和解析>>
科目:初中数学 来源: 题型:
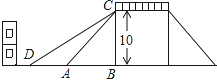
【题目】如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=![]() :3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在坐标平面内△ABC的顶点坐标分别为A(0,2),B(3,3),C(2,1),(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC关于原点对称的△A1B1C1,并直接写出点C1点的坐标;
(2)画出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2,并直接写出C2点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P的坐标为(0,2),直线y=![]() 与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为( )
与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为( )

A.3 B.4 C.5 D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
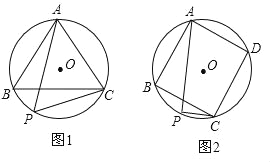
【题目】(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为劣弧BC上一动点.求证:PA=PB+PC;
(2)已知:如图2,四边形ABCD是⊙O的内接正方形,点P为劣弧BC上一动点.求证:PA=PC+![]() PB.
PB.
查看答案和解析>>
科目:初中数学 来源: 题型:
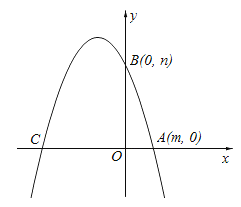
【题目】已知一元二次方程x2﹣4x+3=0的两根是m,n且m<n.如图,若抛物线y=﹣x2+bx+c的图象经过点A(m,0)、B(0,n).
(1)求抛物线的解析式.
(2)若(1)中的抛物线与x轴的另一个交点为C.根据图象回答,当x取何值时,抛物线的图象在直线BC的上方?
(3)点P在线段OC上,作PE⊥x轴与抛物线交于点E,若直线BC将△CPE的面积分成相等的两部分,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com