
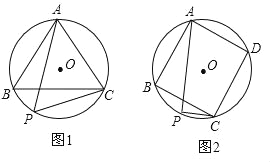
【题目】(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为劣弧BC上一动点.求证:PA=PB+PC;
(2)已知:如图2,四边形ABCD是⊙O的内接正方形,点P为劣弧BC上一动点.求证:PA=PC+![]() PB.
PB.
【答案】(1)证明见解析 (2)证明见解析
【解析】
(1)延长BP至E,使PE=PC,连接CE,证明△PCE是等边三角形.利用CE=PC,∠BCE=∠ACP,BC=AC,得到△BEC≌△APC,所以PA=BE=PB+PC;
(2)过点B作BE⊥PB交PA于E,证明△ABE≌△CBP,所以PC=AE,可得PA=PC+![]() PB.
PB.
证明:(1)延长BP至E,使PE=PC,连接CE,如图1,
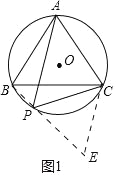
∵A、B、P、C四点共圆,
∴∠BAC+∠BPC=180°,
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP,
∵△ABC、△ECP为等边三角形,
∴CE=PC,AC=BC,
在△BEC和△APC中,
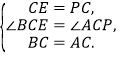
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC;
(2)过点B作BE⊥PB交PA于E,如图2,

∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
∴∠APB=45°,
∴BP=BE,
∴PE=![]() PB,
PB,
在△ABE和△CBP中,
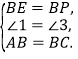
∴△ABE≌△CBP(SAS),
∴PC=AE,
∴PA=AE+PE=PC+![]() PB.
PB.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
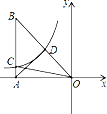
【题目】如图,已知反比函数![]() 的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于C,连结AD、OC,若△ABO的周长为
的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于C,连结AD、OC,若△ABO的周长为![]() ,AD=2,则△ACO的面积为( )
,AD=2,则△ACO的面积为( )
A. ![]() B. 1 C. 2 D. 4
B. 1 C. 2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】吴京同学根据学习函数的经验,对一个新函数![]() 的图象和性质进行了如下探究,请帮他把探究过程补充完整.
的图象和性质进行了如下探究,请帮他把探究过程补充完整.
(1)该函数的自变量![]() 的取值范围是______.
的取值范围是______.
(2)列表:
| … |
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| … |
|
|
|
|
|
|
|
|
| … |
表中![]() ________,
________,![]() _______.
_______.
(3)描点、连线
在下面的格点图中,建立适当的平面直角坐标系![]() 中,描出上表中各对对应值为坐标的点(其中
中,描出上表中各对对应值为坐标的点(其中![]() 为横坐标,
为横坐标,![]() 为纵坐标),并根据描出的点画出该函数的图象:
为纵坐标),并根据描出的点画出该函数的图象:

(4)观察所画出的函数图象,写出该函数的两条性质:
①_______________________________________;
②_______________________________________.
(5)函数![]() 与直线
与直线![]() 的交点有2个,那么
的交点有2个,那么![]() 的取值范围_________.
的取值范围_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
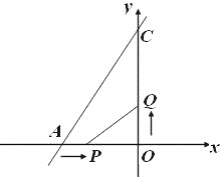
【题目】如图,已知,在直角坐标系xOy中,直线 y=![]() x+8与x轴、y轴分别交于点A、C,点P从A点开始以1个单位/秒的速度沿x轴向右移动,点Q从O点开始以2个单位/秒的速度沿y轴向上移动,如果P、Q两点同时出发,经过几秒钟,能使△PQO的面积为8个平方单位.com
x+8与x轴、y轴分别交于点A、C,点P从A点开始以1个单位/秒的速度沿x轴向右移动,点Q从O点开始以2个单位/秒的速度沿y轴向上移动,如果P、Q两点同时出发,经过几秒钟,能使△PQO的面积为8个平方单位.com
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抽屉里放有4只白袜子和2只黑袜子.
(1)从中任意摸出1只袜子,记下颜色后放回,搅匀,再摸出1只袜子,摸出的两只袜子颜色相同的概率是多少.
(2)若第一次摸出不放回,摸出的两只袜子颜色相同的概率是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
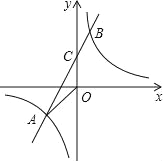
【题目】如图,已知A(n,﹣2),B(1,4)是一次函数y=kx+b的图象与反比例函数y=![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的解析式;
(2)求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
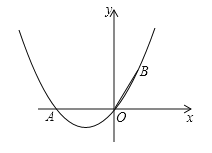
【题目】如图,在直角坐标系中,点A的坐标为(-2,0),OB=OA,且∠AOB=120°.
(1)求经过A、O、B三点的抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点C,使△OBC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;
(3)若点M为抛物线上一点,点N为对称轴上一点,是否存在点M、N使得A、O、M、N构成的四边形是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组研究某型号冷柜温度的变化情况,发现该冷柜的工作过程是:当温度达到设定温度![]() ℃时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到
℃时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到![]() ℃时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至
℃时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至![]() ℃时,制冷再次停止,…,按照以上方式循环进行.同学们记录
℃时,制冷再次停止,…,按照以上方式循环进行.同学们记录![]() 内9个时间点冷柜中的温度
内9个时间点冷柜中的温度![]() (℃)随时间
(℃)随时间![]() 变化情况,制成下表:
变化情况,制成下表:
时间 | … | 4 | 8 | 10 | 16 | 20 | 21 | 22 | 23 | 24 | … |
温度 | … |
|
|
|
|
|
|
|
|
| … |
(1)如图,在直角坐标系中,描出上表数据对应的点,并画出当![]() 时温度
时温度![]() 随时间
随时间![]() 变化的函数图象;
变化的函数图象;
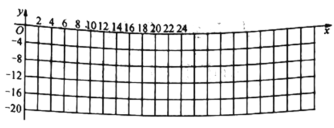
(2)通过图表分析发现,冷柜中的温度![]() 是时间
是时间![]() 的函数.
的函数.
①当![]() 时,写出符合表中数据的函数解析式;
时,写出符合表中数据的函数解析式;
②当![]() 时,写出符合表中数据的函数解析式;
时,写出符合表中数据的函数解析式;
(3)当前冷柜的温度![]() ℃时,冷柜继续工作36分钟,此时冷柜中的温度是多少?
℃时,冷柜继续工作36分钟,此时冷柜中的温度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com