
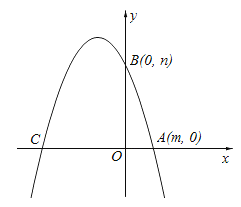
ЁОЬтФПЁПвбжЊвЛдЊЖўДЮЗНГЬx2Љ4x+3=0ЕФСНИљЪЧmЃЌnЧвmЃМnЃЎШчЭМЃЌШєХзЮяЯпy=Љx2+bx+cЕФЭМЯѓОЙ§ЕуAЃЈmЃЌ0ЃЉЁЂBЃЈ0ЃЌnЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ2ЃЉШєЃЈ1ЃЉжаЕФХзЮяЯпгыxжсЕФСэвЛИіНЛЕуЮЊCЃЎИљОнЭМЯѓЛиД№ЃЌЕБxШЁКЮжЕЪБЃЌХзЮяЯпЕФЭМЯѓдкжБЯпBCЕФЩЯЗНЃП
ЃЈ3ЃЉЕуPдкЯпЖЮOCЩЯЃЌзїPEЁЭxжсгыХзЮяЯпНЛгкЕуEЃЌШєжБЯпBCНЋЁїCPEЕФУцЛ§ЗжГЩЯрЕШЕФСНВПЗжЃЌЧѓЕуPЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=Љx2Љ2x+3ЃЛЃЈ2ЃЉЉ3ЃМxЃМ0ЃЛЃЈ3ЃЉЃЈЉ1ЃЌ0ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЧѓГіЗНГЬЕФНтЃЌЕУЕНAЁЂBЕФзјБъЃЌДњШыХзЮяЯпЕУЕНЗНГЬзщЃЌЧѓГіЗНГЬзщЕФНтМДПЩЃЛ
ЃЈ2ЃЉЧѓГіCЕФзјБъЃЌИљОнBЁЂCЕФзјБъЧѓГіМДПЩЃЛ
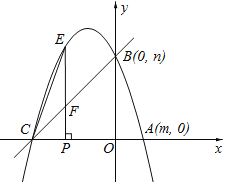
ЃЈ3ЃЉЩшжБЯпBCНЛPEгкFЃЌPЕузјБъЮЊЃЈaЃЌ0ЃЉЃЌдђEЕузјБъЮЊЃЈaЃЌЉa2Љ2a+3ЃЉЃЌИљОнШ§НЧаЮЕФУцЛ§ЧѓГіFЕФзјБъЃЌЩшжБЯпBCЕФНтЮіЪНЪЧy=kx+bЃЌАбBЁЂCЕФзјБъДњШыЧѓГіжБЯпBCЃЌАбFЕФзјБъДњШыЧѓГіМДПЩЃЎ
ЃЈ1ЃЉЁпx2Љ4x+3=0ЕФСНИіИљЮЊ x1=1ЃЌx2=3ЃЌЁрAЕуЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЌBЕуЕФзјБъЮЊЃЈ0ЃЌ3ЃЉЃЎ
гжЁпХзЮяЯпy=Љx2+bx+cЕФЭМЯѓОЙ§ЕуAЃЈ1ЃЌ0ЃЉЁЂBЃЈ0ЃЌ3ЃЉСНЕуЃЌЁр![]() ЃЌЕУЃК
ЃЌЕУЃК![]() ЃЌЁрХзЮяЯпЕФНтЮіЪНЮЊy=Љx2Љ2x+3ЃЎ
ЃЌЁрХзЮяЯпЕФНтЮіЪНЮЊy=Љx2Љ2x+3ЃЎ
ЃЈ2ЃЉзїжБЯпBCЃЌгЩЃЈ1ЃЉЕУЃКy=Љx2Љ2x+3ЃЎ
ЁпХзЮяЯпy=Љx2Љ2x+3гыxжсЕФСэвЛИіНЛЕуЮЊCЃЌСюЉx2Љ2x+3=0ЃЌНтЕУЃКx1=1ЃЌx2=Љ3ЃЌЁрCЕуЕФзјБъЮЊЃЈЉ3ЃЌ0ЃЉЃЌгЩЭМПЩжЊЃКЕБЉ3ЃМxЃМ0ЪБЃЌХзЮяЯпЕФЭМЯѓдкжБЯпBCЕФЩЯЗНЃЎ
ЃЈ3ЃЉЩшжБЯпBCНЛPEгкFЃЌPЕузјБъЮЊЃЈaЃЌ0ЃЉЃЌдђEЕузјБъЮЊЃЈaЃЌЉa2Љ2a+3ЃЉЃЎ
ЁпжБЯпBCНЋЁїCPEЕФУцЛ§ЗжГЩЯрЕШЕФСНВПЗжЃЌЁрFЪЧЯпЖЮPEЕФжаЕуЃЈИљОнЕШЕзЕШИпЕФШ§НЧаЮЕФУцЛ§ЯрЕШЃЉЃЌМДFЕуЕФзјБъЪЧЃЈaЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁпжБЯпBCЙ§ЕуBЃЈ0.3ЃЉКЭCЃЈЉ3ЃЌ0ЃЉЃЌЩшжБЯпBCЕФНтЮіЪНЪЧy=kx+bЃЈkЁй0ЃЉЃЌДњШыЕУЃК![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁржБЯпBCЕФНтЮіЪНЮЊy=x+3ЃЎ
ЃЌЁржБЯпBCЕФНтЮіЪНЮЊy=x+3ЃЎ
ЁпЕуFдкжБЯпBCЩЯЃЌЁрЕуFЕФзјБъТњзужБЯпBCЕФНтЮіЪНЃЌМД![]() =a+3ЃЌ
=a+3ЃЌ
НтЕУЃКa1=Љ1ЃЌa2=Љ3ЃЈДЫЪБPЕугыЕуCжиКЯЃЌЩсШЅЃЉЃЌЁрPЕуЕФзјБъЪЧЃЈЉ1ЃЌ0ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮтОЉЭЌбЇИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдвЛИіаТКЏЪ§![]() ЕФЭМЯѓКЭаджЪНјааСЫШчЯТЬНОПЃЌЧыАяЫћАбЬНОПЙ§ГЬВЙГфЭъећЃЎ
ЕФЭМЯѓКЭаджЪНјааСЫШчЯТЬНОПЃЌЧыАяЫћАбЬНОПЙ§ГЬВЙГфЭъећЃЎ
ЃЈ1ЃЉИУКЏЪ§ЕФздБфСП![]() ЕФШЁжЕЗЖЮЇЪЧ______ЃЎ
ЕФШЁжЕЗЖЮЇЪЧ______ЃЎ
ЃЈ2ЃЉСаБэЃК
| Ё |
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | Ё |
| Ё |
|
|
|
|
|
|
|
|
| Ё |
Бэжа![]() ________ЃЌ
________ЃЌ![]() _______ЃЎ
_______ЃЎ
ЃЈ3ЃЉУшЕуЁЂСЌЯп
дкЯТУцЕФИёЕуЭМжаЃЌНЈСЂЪЪЕБЕФЦНУцжБНЧзјБъЯЕ![]() жаЃЌУшГіЩЯБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЈЦфжа
жаЃЌУшГіЩЯБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЈЦфжа![]() ЮЊКсзјБъЃЌ
ЮЊКсзјБъЃЌ![]() ЮЊзнзјБъЃЉЃЌВЂИљОнУшГіЕФЕуЛГіИУКЏЪ§ЕФЭМЯѓЃК
ЮЊзнзјБъЃЉЃЌВЂИљОнУшГіЕФЕуЛГіИУКЏЪ§ЕФЭМЯѓЃК

ЃЈ4ЃЉЙлВьЫљЛГіЕФКЏЪ§ЭМЯѓЃЌаДГіИУКЏЪ§ЕФСНЬѕаджЪЃК
Ђй_______________________________________ЃЛ
Ђк_______________________________________ЃЎ
ЃЈ5ЃЉКЏЪ§![]() гыжБЯп
гыжБЯп![]() ЕФНЛЕуга2ИіЃЌФЧУД
ЕФНЛЕуга2ИіЃЌФЧУД![]() ЕФШЁжЕЗЖЮЇ_________ЃЎ
ЕФШЁжЕЗЖЮЇ_________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
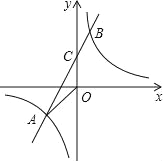
ЁОЬтФПЁПШчЭМЃЌвбжЊAЃЈnЃЌЉ2ЃЉЃЌBЃЈ1ЃЌ4ЃЉЪЧвЛДЮКЏЪ§y=kx+bЕФЭМЯѓгыЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓЕФСНИіНЛЕуЃЌжБЯпABгыyжсНЛгкЕуCЃЎ
ЕФЭМЯѓЕФСНИіНЛЕуЃЌжБЯпABгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЁїAOCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌЕуAЕФзјБъЮЊЃЈ-2ЃЌ0ЃЉЃЌOB=OAЃЌЧвЁЯAOB=120ЁуЃЎ
ЃЈ1ЃЉЧѓОЙ§AЁЂOЁЂBШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉжаХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдкЕуCЃЌЪЙЁїOBCЕФжмГЄзюаЁЃПШєДцдкЃЌЧѓГіЕуCЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЕуMЮЊХзЮяЯпЩЯвЛЕуЃЌЕуNЮЊЖдГЦжсЩЯвЛЕуЃЌЪЧЗёДцдкЕуMЁЂNЪЙЕУAЁЂOЁЂMЁЂNЙЙГЩЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧѓГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
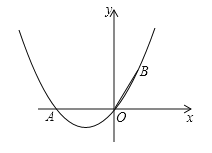
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп yЃНax2Љ5ax+c НЛ x жсгкЕу AЃЌЕу A ЕФзјБъЮЊЃЈ4ЃЌ0ЃЉЃЎ
(1)гУКЌ a ЕФДњЪ§ЪНБэЪО cЃЎ
(2)ЕБ aЃН![]() ЪБЃЌЧѓ x ЮЊКЮжЕЪБ y ШЁЕУзюаЁжЕЃЌВЂЧѓГі y ЕФзюаЁжЕЃЎ
ЪБЃЌЧѓ x ЮЊКЮжЕЪБ y ШЁЕУзюаЁжЕЃЌВЂЧѓГі y ЕФзюаЁжЕЃЎ
(3)ЕБ aЃН![]() ЪБЃЌЧѓ 0ЁмxЁм6 ЪБ y ЕФШЁжЕЗЖЮЇЃЎ
ЪБЃЌЧѓ 0ЁмxЁм6 ЪБ y ЕФШЁжЕЗЖЮЇЃЎ
(4)вбжЊЕу B ЕФзјБъЮЊЃЈ0ЃЌ3ЃЉЃЌЕБХзЮяЯпЕФЖЅЕуТфдкЁїAOB ЭтНгдВФкВПЪБЃЌжБНгаДГі aЕФШЁжЕЗЖЮЇЃЎ
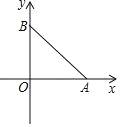
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
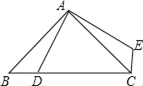
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЕуDдкBCБпЩЯЃЌЁїABDШЦЕуAа§зЊКѓгыЁїACEжиКЯЃЌШчЙћЁЯECB=100ЁуЃЌФЧУДа§зЊНЧЕФДѓаЁЪЧ_____ЁуЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЮяСїЙЋЫОвЊАб3000ЖжЛѕЮяДгMЪадЫЕНWЪаЃЎЃЈУПШеЕФдЫЪфСПЮЊЙЬЖЈжЕЃЉ
ЃЈ1ЃЉДгдЫЪфПЊЪМЃЌУПЬьдЫЪфЕФЛѕЮяЖжЪ§yЃЈЕЅЮЛЃКЖжЃЉгыдЫЪфЪБМфxЃЈЕЅЮЛЃКЬьЃЉжЎМфгадѕбљЕФКЏЪ§ЙиЯЕЪНЃП
ЃЈ2ЃЉвђЪмЕНбиЯпЕРТЗИФРЉНЈЙЄГЬгАЯьЃЌЪЕМЪУПЬьЕФдЫЪфСПБШдМЦЛЎЩй20%ЃЌвджТЭЦГй1ЬьЭъГЩдЫЪфШЮЮёЃЌЧѓдМЦЛЎЭъГЩдЫЪфШЮЮёЕФЬьЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪ§бЇаЫШЄаЁзщбаОПФГаЭКХРфЙёЮТЖШЕФБфЛЏЧщПіЃЌЗЂЯжИУРфЙёЕФЙЄзїЙ§ГЬЪЧЃКЕБЮТЖШДяЕНЩшЖЈЮТЖШ![]() ЁцЪБЃЌжЦРфЭЃжЙЃЌДЫКѓРфЙёжаЕФЮТЖШПЊЪМж№НЅЩЯЩ§ЃЌЕБЩЯЩ§ЕН
ЁцЪБЃЌжЦРфЭЃжЙЃЌДЫКѓРфЙёжаЕФЮТЖШПЊЪМж№НЅЩЯЩ§ЃЌЕБЩЯЩ§ЕН![]() ЁцЪБЃЌжЦРфПЊЪМЃЌЮТЖШПЊЪМж№НЅЯТНЕЃЌЕБРфЙёздЖЏжЦРфжС
ЁцЪБЃЌжЦРфПЊЪМЃЌЮТЖШПЊЪМж№НЅЯТНЕЃЌЕБРфЙёздЖЏжЦРфжС![]() ЁцЪБЃЌжЦРфдйДЮЭЃжЙЃЌЁЃЌАДеевдЩЯЗНЪНбЛЗНјааЃЎЭЌбЇУЧМЧТМ
ЁцЪБЃЌжЦРфдйДЮЭЃжЙЃЌЁЃЌАДеевдЩЯЗНЪНбЛЗНјааЃЎЭЌбЇУЧМЧТМ![]() Фк9ИіЪБМфЕуРфЙёжаЕФЮТЖШ
Фк9ИіЪБМфЕуРфЙёжаЕФЮТЖШ![]() ЃЈЁцЃЉЫцЪБМф
ЃЈЁцЃЉЫцЪБМф![]() БфЛЏЧщПіЃЌжЦГЩЯТБэЃК
БфЛЏЧщПіЃЌжЦГЩЯТБэЃК
ЪБМф | Ё | 4 | 8 | 10 | 16 | 20 | 21 | 22 | 23 | 24 | Ё |
ЮТЖШ | Ё |
|
|
|
|
|
|
|
|
| Ё |
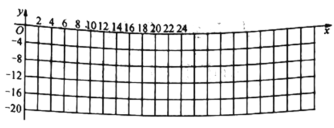
ЃЈ1ЃЉШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌУшГіЩЯБэЪ§ОнЖдгІЕФЕуЃЌВЂЛГіЕБ![]() ЪБЮТЖШ
ЪБЮТЖШ![]() ЫцЪБМф
ЫцЪБМф![]() БфЛЏЕФКЏЪ§ЭМЯѓЃЛ
БфЛЏЕФКЏЪ§ЭМЯѓЃЛ
ЃЈ2ЃЉЭЈЙ§ЭМБэЗжЮіЗЂЯжЃЌРфЙёжаЕФЮТЖШ![]() ЪЧЪБМф
ЪЧЪБМф![]() ЕФКЏЪ§ЃЎ
ЕФКЏЪ§ЃЎ
ЂйЕБ![]() ЪБЃЌаДГіЗћКЯБэжаЪ§ОнЕФКЏЪ§НтЮіЪНЃЛ
ЪБЃЌаДГіЗћКЯБэжаЪ§ОнЕФКЏЪ§НтЮіЪНЃЛ
ЂкЕБ![]() ЪБЃЌаДГіЗћКЯБэжаЪ§ОнЕФКЏЪ§НтЮіЪНЃЛ
ЪБЃЌаДГіЗћКЯБэжаЪ§ОнЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ3ЃЉЕБЧАРфЙёЕФЮТЖШ![]() ЁцЪБЃЌРфЙёМЬајЙЄзї36ЗжжгЃЌДЫЪБРфЙёжаЕФЮТЖШЪЧЖрЩйЃП
ЁцЪБЃЌРфЙёМЬајЙЄзї36ЗжжгЃЌДЫЪБРфЙёжаЕФЮТЖШЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
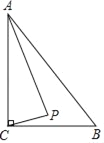
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABC жаЃЌЁЯACBЃН90ЁуЃЌACЃН6ЃЌBCЃН4ЃЌЕуPЪЧЁїABCФкВПЕФвЛИіЖЏЕуЃЌЧвТњзуЁЯPACЃНЁЯPCBЃЌдђЯпЖЮBPГЄЕФзюаЁжЕЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com