
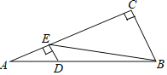
【题目】如图,在△ABC中,∠C=90°,∠A=30°,D为AB上一点,且AD:DB=1:3,DE⊥AC于点E,连接BE,则tan∠CBE的值等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】如图,AD是直角三角形ABC斜边上的中线,AE⊥AD交CB延长线于E,则图中一定相似的三角形是( )
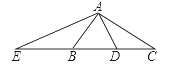
A. △AED与△ACB B. △AEB与△ACD C. △BAE与△ACE D. △AEC与△DAC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,B的坐标分别为(-2,3)和(1,3),抛物线y=ax2+bx+c(a<0)的 顶点在线段AB上运动时,形状保持不变,且与x轴交于C,D两点(C在D的左侧),给出下列结论:①c<3;②当x<-3时,y随x的增大而增大;③若点D的横坐标最大值为5,则点C的横坐标最小值为-5;④当四边形ACDB为平行四边形时,a=![]() .其中正确的是( )
.其中正确的是( )
A. ②④ B. ②③ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
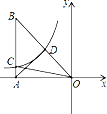
【题目】如图,已知反比函数![]() 的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于C,连结AD、OC,若△ABO的周长为
的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于C,连结AD、OC,若△ABO的周长为![]() ,AD=2,则△ACO的面积为( )
,AD=2,则△ACO的面积为( )
A. ![]() B. 1 C. 2 D. 4
B. 1 C. 2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们把横、纵坐标均为整数的点叫做整点.已知反比例函数y=![]() (m<0)与y=x2﹣4在第四象限内围成的封闭图形(包括边界)内的整点的个数为2,则实数m的取值范围为__.
(m<0)与y=x2﹣4在第四象限内围成的封闭图形(包括边界)内的整点的个数为2,则实数m的取值范围为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
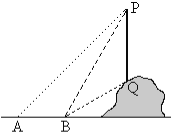
【题目】如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度.他们采取的方法是:先在地面上的点A处测得杆顶端点P的仰角是45°,再向前走到B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°,这时只需要测出AB的长度就能通过计算求出电线杆PQ的高度.你同意他们的测量方案吗?若同意,画出计算时的图形,简要写出计算的思路,不用求出具体值;若不同意,提出你的测量方案,并简要写出计算思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】吴京同学根据学习函数的经验,对一个新函数![]() 的图象和性质进行了如下探究,请帮他把探究过程补充完整.
的图象和性质进行了如下探究,请帮他把探究过程补充完整.
(1)该函数的自变量![]() 的取值范围是______.
的取值范围是______.
(2)列表:
| … |
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| … |
|
|
|
|
|
|
|
|
| … |
表中![]() ________,
________,![]() _______.
_______.
(3)描点、连线
在下面的格点图中,建立适当的平面直角坐标系![]() 中,描出上表中各对对应值为坐标的点(其中
中,描出上表中各对对应值为坐标的点(其中![]() 为横坐标,
为横坐标,![]() 为纵坐标),并根据描出的点画出该函数的图象:
为纵坐标),并根据描出的点画出该函数的图象:

(4)观察所画出的函数图象,写出该函数的两条性质:
①_______________________________________;
②_______________________________________.
(5)函数![]() 与直线
与直线![]() 的交点有2个,那么
的交点有2个,那么![]() 的取值范围_________.
的取值范围_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
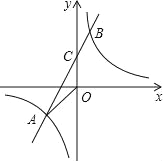
【题目】如图,已知A(n,﹣2),B(1,4)是一次函数y=kx+b的图象与反比例函数y=![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的解析式;
(2)求△AOC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com