
【题目】已知,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 和过点
和过点![]() 的切线互相垂直,垂足为点
的切线互相垂直,垂足为点![]() .
.
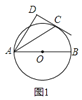
![]() 如图
如图![]() ,求证:
,求证:![]() 平分
平分![]() ;
;
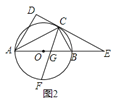
![]() 如图
如图![]() ,直线
,直线![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
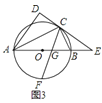
![]() 在
在![]() 的条件下,如图
的条件下,如图![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】![]() 证明见解析;(2)证明见解析;(3)
证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)连接OC,根据切线与圆的关系和直角三角形内角之间的关系,可以推出AC平分∠DAB;
(2)根据圆周角定理以及三角形的外角的性质定理证明∠ECG=∠EGC,根据等角对等边即可证得;
(3)证明△ECB∽△EAC,根据相似三角形的性质求得![]() ,在直角△EOC中利用勾股定理列方程求得BE和CE,进而求得BG,然后根据△AGF∽△CGB,根据相似三角形的性质求得FG的长.
,在直角△EOC中利用勾股定理列方程求得BE和CE,进而求得BG,然后根据△AGF∽△CGB,根据相似三角形的性质求得FG的长.
![]() 证明:连接
证明:连接![]() ,如图
,如图![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
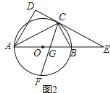
即![]() 平分
平分![]() ;
;
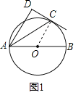
![]() 证明:如图
证明:如图![]() ,∵
,∵![]() 是
是![]() 的切线,
的切线,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 解:如图
解:如图![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.

∵![]() 是直径,
是直径,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() 是直径,
是直径,
∴![]() .
.
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
设![]() ,则
,则![]() ,在
,在![]() 中,
中,![]() ,
,
解得![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】小明将三角形纸片ABC(AB >AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图①);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图②).小明认为△AEF是等腰三角形,你同意吗?如果同意,请你给出证明,如果不同意,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,∠CAP=∠APQ,PR=PS,下面的结论:①AS=AR;②QP∥AR;③△BRP≌△CSP.其中正确的是( )

A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有16个只有颜色不同的球,其中红球有x个,白球有2x个,其他均为黄球,现甲从布袋中随机摸出一个球,若是红球则甲同学获胜,甲同学把摸出的球放回并搅匀,由乙同学随机摸出一个球,若为黄球,则乙同学获胜。
(1)当X=3时,谁获胜的可能性大?
(2)当x为何值时,游戏对双方是公平的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC,若CE=5,则BC等于( )
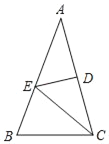
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
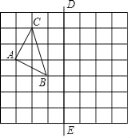
【题目】如图,在所给的网格图中,完成下列各题(用直尺画图,否则不给分)
(1)画出格点△ABC关于直线DE的对称的△A1B1C1;
(2)在DE上画出点P,使PA+PC最小;
(3)在DE上画出点Q,使QA﹣QB最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,分别沿长方形纸片
,分别沿长方形纸片![]() 和正方形纸片
和正方形纸片![]() 的对角线
的对角线![]() ,
,![]() 剪开,拼成如图
剪开,拼成如图![]() 所示的四边形
所示的四边形![]() ,若中间空白部分四边形恰好是正方形
,若中间空白部分四边形恰好是正方形![]() ,且四边形
,且四边形![]() 的面积为
的面积为![]() ,则正方形的面积是( )
,则正方形的面积是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=![]() ,点B的坐标为(m,-2).
,点B的坐标为(m,-2).
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.

【答案】(1)△AHO的周长为12;(2) 反比例函数的解析式为y=![]() ,一次函数的解析式为y=-
,一次函数的解析式为y=-![]() x+1.
x+1.
【解析】试题分析: (1)根据正切函数,可得AH的长,根据勾股定理,可得AO的长,根据三角形的周长,可得答案;
(2)根据待定系数法,可得函数解析式.
试题解析:(1)由OH=3,tan∠AOH=![]() ,得
,得
AH=4.即A(-4,3).
由勾股定理,得
AO=![]() =5,
=5,
△AHO的周长=AO+AH+OH=3+4+5=12;
(2)将A点坐标代入y=![]() (k≠0),得
(k≠0),得
k=-4×3=-12,
反比例函数的解析式为y=![]() ;
;
当y=-2时,-2=![]() ,解得x=6,即B(6,-2).
,解得x=6,即B(6,-2).
将A、B点坐标代入y=ax+b,得
![]() ,
,
解得 ,
,
一次函数的解析式为y=-![]() x+1.
x+1.
考点:反比例函数与一次函数的交点问题.
【题型】解答题
【结束】
25
【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
求证:①AB=AD;
②CD平分∠ACE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com