Question

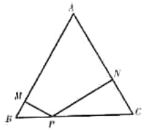
【题目】在边长为的等边三角形中，是边上任意一点，过点分别作，，、分别为垂足．

（1）求证：不论点在边的何处时都有的长恰好等于三角形一边上的高；

（2）当的长为何值时，四边形的面积最大，并求出最大值．

Answer 1

【答案】（1）PM+PN=CD；（2）1，.

【解析】

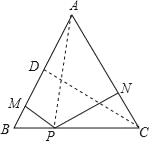
试题分析：（1）连接AP，过C作CD⊥AB于D，根据等边三角形的性质得到AB=AC，根据三角形的面积公式列方程即可得到结论；

（2）设BP=x，则CP=2﹣x，由△ABC是等边三角形，得到∠B=∠C=60°，解直角三角形得到BM=x，PM=x，CN=（2﹣x），PN=（2﹣x），根据二次函数的性质即可得到结论．

试题解析：（1）连接AP，过C作CD⊥AB于D，

∵△ABC是等边三角形，

∴AB=AC，

∵S△ABC=S△ABP+S△ACP，

∴AB·CD=AB·PM+AC·PN，

∴PM+PN=CD，

即不论点P在BC边的何处时都有PM+PN的长恰好等于三角形ABC一边上的高；

（2）设BP=x，则CP=2﹣x，

∵△ABC是等边三角形，

∴∠B=∠C=60°，

∵PM⊥AB，PN⊥AC，

∴BM=x，PM=x，CN=（2﹣x），PN=（2﹣x），

∴四边形AMPN的面积=×（2﹣x）x+ [2﹣（2﹣x）]·（2﹣x）=，

∴当BP=1时，四边形AMPN的面积最大，最大值是．