
| 1 |
| 2 |
| AP |
| BQ |
| AO |
| OB |
| 2t-21 |
| 16-t |
| 1 |
| 2 |
| 58 |
| 5 |
| PF |
| FQ |
| DC |
| CB |

| 1 |
| 2 |
| 1 |
| 2 |
| AP |
| BQ |
| AO |
| OB |
| 2t-21 |
| 16-t |
| 1 |
| 2 |
| 58 |
| 5 |
| 58 |
| 5 |
| QE |
| PE |
| 30 |
| 29 |
| PF |
| FQ |
| DC |
| CB |
| t |
| 12 |
| 12 |
| 16 |


科目:初中数学 来源: 题型:
 (2013•张家港市二模)如图,在平面直角坐标系中,点A坐标为(-4,0),⊙O与x轴的负半轴交于B(-2,0).点P是⊙O上的一个动点,PA的中点为Q.当点Q也落在⊙O上时,cos∠OQB的值等于( )
(2013•张家港市二模)如图,在平面直角坐标系中,点A坐标为(-4,0),⊙O与x轴的负半轴交于B(-2,0).点P是⊙O上的一个动点,PA的中点为Q.当点Q也落在⊙O上时,cos∠OQB的值等于( )查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•张家港市二模)如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A、D分别落在A′、D′处,且A′D′经过B,EF为折痕,当D′F⊥CD时,
(2013•张家港市二模)如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A、D分别落在A′、D′处,且A′D′经过B,EF为折痕,当D′F⊥CD时,| FD |
| FC |
查看答案和解析>>
科目:初中数学 来源: 题型:
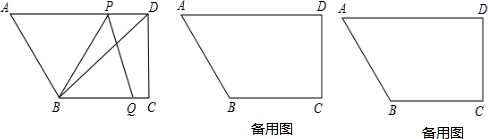
 (2013•张家港市二模)如图,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=2AD,F、E分别是BA、BC的中点,则下列结论正确的是
(2013•张家港市二模)如图,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=2AD,F、E分别是BA、BC的中点,则下列结论正确的是| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com