
【题目】已知:如图所示,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 平分
平分![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() .
.
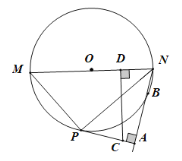
(1)求证:![]() 与
与![]() 相切;
相切;
(2)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)若![]() 是
是![]() 中点,过
中点,过![]() 作
作![]() 交
交![]() 于
于![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
【答案】(1)见解析; (2)![]() ;(3)半径
;(3)半径![]()
【解析】
(1)连接OP,根据角平分线的性质及圆的半径相等的性质得到![]() ,推出OP∥AN,根据
,推出OP∥AN,根据![]() 即可得到OP⊥PA,由此得到结论;
即可得到OP⊥PA,由此得到结论;
(2)连接![]() 交
交![]() 于
于![]() ,根据勾股定理求出BM=16得到ME=8,再利用勾股定理求出OE=6,得到PE=4,即可利用勾股定理求出MP;
,根据勾股定理求出BM=16得到ME=8,再利用勾股定理求出OE=6,得到PE=4,即可利用勾股定理求出MP;
(3)连接![]() ,设
,设![]() 与
与![]() 的交点为
的交点为![]() ,根据
,根据![]() 设
设![]() ,可求
,可求![]() ,根据角平分线的性质及圆的半径相等的性质得到
,根据角平分线的性质及圆的半径相等的性质得到![]() ,推出PC=FC,根据
,推出PC=FC,根据![]() 求出x=2,即可得到半径OP.
求出x=2,即可得到半径OP.
(1)证明:连接![]() .
.
![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
![]() 与
与![]() 相切;
相切;
(2)解:连接![]() 交
交![]() 于
于![]() ,
,
∵MN是直径,
∴BM⊥BN,
∴OP⊥BM,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)解:连接![]() ,设
,设![]() 与
与![]() 的交点为
的交点为![]() .
.
![]() ,
,
∴可设![]() ,
,
![]() .
.
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
∴半径![]() .
.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG、BG、DG,下列结论中错误的是( )
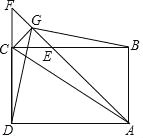
A.BC=DFB.△DCG≌△BGCC.△DFG≌△BCGD.AC:BG=![]() :1
:1
查看答案和解析>>
科目:初中数学 来源: 题型:
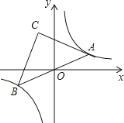
【题目】如图,点A是双曲线![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
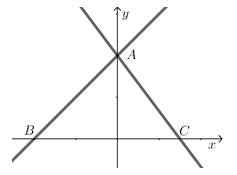
【题目】如图,在平面直角坐标系中,直线y=x+4与y轴交于点A,与x轴交于点B,直线y=kx+b经过点A,且交x轴与点C(3,0).
(1)求直线AC的函数表达式;
(2)动点P在线段CB上由C向B匀速运动,到达点B后停止运动,运动速度为3个单位长度,过点P作PE⊥x轴,交直线AC于点E,过点E作直线GE∥x轴交![]() 轴于点F,交直线AB于点G,设点P的运动时间为t(t>0)秒.
轴于点F,交直线AB于点G,设点P的运动时间为t(t>0)秒.
①直接写出线段PE的长度(用含t的代数式表示);
②当EG=1时,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 、
、![]() 是反比例函数
是反比例函数![]()
![]() 图象上的点,
图象上的点,![]() 于点
于点![]() ,
,![]() .
.
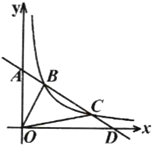
(1)求直线![]() 的函数解析式及反比例函数的解析式;
的函数解析式及反比例函数的解析式;
(2)若![]() 、
、![]() 、
、![]() 的面积分别为
的面积分别为![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() ,
,![]() ,
,![]() 的一个数量关系式.
的一个数量关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题引入:如图1所示,正方形![]() 和正方形
和正方形![]() ,则
,则![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() ;
;
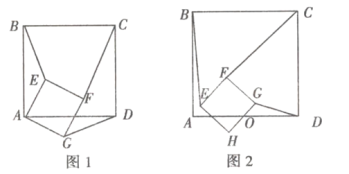
(2)类比探究:如图2所示,![]() 为
为![]() 、
、![]() 的中点,正方形
的中点,正方形![]() 和正方形
和正方形![]() 中,判断
中,判断![]() 和
和![]() 的数量关系,并求出
的数量关系,并求出![]() 的值.
的值.
(3)解决问题:
①若把(1)中的正方形都改成矩形,且![]() ,则(1)中的结论还成立吗?若不能成立,请写出
,则(1)中的结论还成立吗?若不能成立,请写出![]() 与
与![]() 的关系,并求出
的关系,并求出![]() 的值;
的值;
②若把(2)中的正方形也都改成矩形,且![]() ,请直接写出
,请直接写出![]() 和
和![]() 的关系以及
的关系以及![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
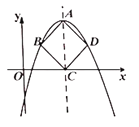
【题目】如图,抛物线![]() (
(![]() )的顶点为
)的顶点为![]() ,对称轴与
,对称轴与![]() 轴交于点
轴交于点![]() ,当以
,当以![]() 为对角线的正方形
为对角线的正方形![]() 的另外两个顶点
的另外两个顶点![]() 、
、![]() 恰好在抛物线上时,我们把这样的抛物线称为美丽抛物线,正方形
恰好在抛物线上时,我们把这样的抛物线称为美丽抛物线,正方形![]() 为它的内接正方形.
为它的内接正方形.
(1)当抛物线![]() 是美丽抛物线时,则
是美丽抛物线时,则![]() ______;当抛物线
______;当抛物线![]() 是美丽抛物线时,则
是美丽抛物线时,则![]() ______;
______;
(2)若抛物线![]() 是美丽抛物线时,则请直接写出
是美丽抛物线时,则请直接写出![]() ,
,![]() 的数量关系;
的数量关系;
(3)若![]() 是美丽抛物线时,(2)
是美丽抛物线时,(2)![]() ,
,![]() 的数量关系成立吗?为什么?
的数量关系成立吗?为什么?
(4)系列美丽抛物线![]() (
(![]() 为小于
为小于![]() 的正整数)顶点在直线
的正整数)顶点在直线![]() 上,且它们中恰有两条美丽抛物线内接正方形面积比为
上,且它们中恰有两条美丽抛物线内接正方形面积比为![]() .求它们二次项系数之和.
.求它们二次项系数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
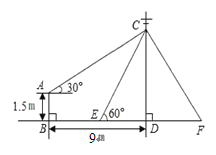
【题目】如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆9m的B处安置高为1.5m的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长.(结果保留根号)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若干名工人某天生产同一种玩具,生产的玩具数整理成条形图(如图所示).则他们生产的玩具数的平均数、中位数、众数分别为( )

A.5,5,4 B.5,5,5
C.5,4,5 D.5,4,4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com