
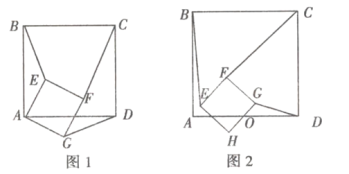
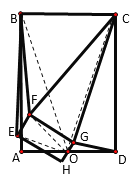
【题目】(1)问题引入:如图1所示,正方形![]() 和正方形
和正方形![]() ,则
,则![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() ;
;
(2)类比探究:如图2所示,![]() 为
为![]() 、
、![]() 的中点,正方形
的中点,正方形![]() 和正方形
和正方形![]() 中,判断
中,判断![]() 和
和![]() 的数量关系,并求出
的数量关系,并求出![]() 的值.
的值.
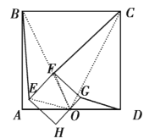
(3)解决问题:
①若把(1)中的正方形都改成矩形,且![]() ,则(1)中的结论还成立吗?若不能成立,请写出
,则(1)中的结论还成立吗?若不能成立,请写出![]() 与
与![]() 的关系,并求出
的关系,并求出![]() 的值;
的值;
②若把(2)中的正方形也都改成矩形,且![]() ,请直接写出
,请直接写出![]() 和
和![]() 的关系以及
的关系以及![]() 的值.
的值.
【答案】(1) ![]() ;(2)
;(2) ![]() ,理由见解析;(3)①结论不成立.此时
,理由见解析;(3)①结论不成立.此时![]() .理由见解析;②
.理由见解析;②![]() .
.
【解析】
(1)根据SAS证明△ABE≌△ADG即可得到BE=DG,连接AC、AF,证明△CAF∽△DAG,即可得到![]() ;
;
(2)连接![]() ,证明△EOH≌△FOG得到
,证明△EOH≌△FOG得到![]() ,再证明
,再证明![]() ,得到
,得到![]() ,得到BE=FC,再证明
,得到BE=FC,再证明![]() 即可求出
即可求出![]() ;
;
(3)①证明![]() 得到BE=3DG,连接
得到BE=3DG,连接![]() ,根据tan∠FAG=tan∠CAD=3,证明
,根据tan∠FAG=tan∠CAD=3,证明![]() ,根据
,根据![]() 证明
证明![]() ,得到
,得到![]() ;
;
②连接![]() ,证明△EOH≌△FOG得到
,证明△EOH≌△FOG得到![]() ,再证明
,再证明![]() ,得到
,得到![]() ,得到BE=FC,再证明
,得到BE=FC,再证明![]() 即可求出
即可求出![]() .
.
(1) ∵四边形ABCD与四边形AEFG都是正方形,
∴AB=AD,AE=AG,∠BAD=∠EAG=90°,
∴∠BAD-∠EAD=∠EAG-∠EAD,
即∠BAE=∠DAG,
∴△ABE≌△ADG,
∴BE=DG,
连接AC、AF,则![]() ,
,![]() ,
,
∵∠CAD=∠FAG=45°,
∴∠CAD-∠FAD=∠FAG-∠FAD,
∴∠CAF=∠DAG,
∴△CAF∽△DAG,
∴![]()
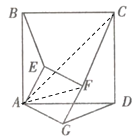
(2)![]() .
.
理由如下:连接![]()
∵正方形![]() 是
是![]() 中点,
中点,
![]() .
.
![]() .
.
![]() .
.
同理:![]()
又![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
又![]() ,
,
![]() ,
,
又![]()
![]()
![]()
![]()
(3)①结论不成立.此时![]() .
.
理由如下:由题可得![]() ,
,
![]() .
.
又![]()
![]() .
.
![]() .
.
连接![]()
![]() ,
,
![]() .
.
![]()
又![]() ,
,
![]() .
.
![]()
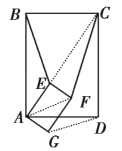
②![]() ,
,
理由如下:连接![]() ,
,
∵矩形![]() 是
是![]() 中点,
中点,
![]() .
.
![]() .
.
![]() .
.
同理:![]()
又![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
又![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵AB=CD,
∴![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系,根据图象解决以下问题:
(1)慢车的速度为_____km/h,快车的速度为_____km/h;
(2)解释图中点C的实际意义并求出点C的坐标;
(3)求当x为多少时,两车之间的距离为500km.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动.在一个不透明的箱子里放有4个完全相同的小球,球上分别标有“0元”、“10元”、“30元”和“50元”的字样.规定:顾客在本商场同一日内,消费每满300元,就可以从箱子里先后摸出两个球(每次只摸出一个球,第一次摸出后不放回).商场根据两个小球所标金额之和返还相应价格的购物券,可以重新在本商场消费.某顾客消费刚好满300元,则在本次消费中:
(1)该顾客至少可得___元购物券,至多可得___元购物券;
(2)请用画树状图或列表法,求出该顾客所获购物券的金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市以3元/本的价格购进某种笔记本若干,然后以5元/本的价格出售,每天售出20本.通过调查发现,这种笔记本的售价每降低0.1元,每天可多售出4本,为保证每天至少售出50本,该超市决定降价销售.
(1)若每本降价![]() 元,则每天的销售量是________本(用含
元,则每天的销售量是________本(用含![]() 的代数式表示).
的代数式表示).
(2)要想每天赢利60元,该超市需将每本的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生食堂共有座位![]() 个,某天午餐时,食堂中学生人数
个,某天午餐时,食堂中学生人数![]() (人)与时间
(人)与时间![]() (分钟)
(分钟)
变化的函数关系图象如图中的折线![]() .
.
(1)试分别求出当![]() 与
与![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)已知该校学生数有![]() 人,考虑到安全因素,学校决定对剩余
人,考虑到安全因素,学校决定对剩余![]() 名同学延时用餐,即等食堂空闲座位不少于
名同学延时用餐,即等食堂空闲座位不少于![]() 个时,再通知剩余
个时,再通知剩余![]() 名同学用餐.请结合图象分析,这
名同学用餐.请结合图象分析,这![]() 名学生至少要延时多少分钟?
名学生至少要延时多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
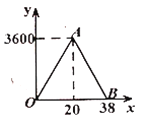
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(1,t+1),B(t-5,-1)两点.
的图象交于A(1,t+1),B(t-5,-1)两点.
(1)求一次函数和反比例函数的解析式;
(2)若点(c,p)和(n,q)是反比例函数y=![]() 图象上任意两点,且满足c=n+1时,求
图象上任意两点,且满足c=n+1时,求![]() 的值.
的值.
(3)若点M(x1,y1)和N(x2,y2)在直线AB(不与A、B重合)上,过M、N两点分别作y轴的平行线交双曲线于E、F,已知x1<-3,0<x2<1,当x1x2=-3时,判断四边形NFEM的形状.并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com