
【题目】某商场为了吸引顾客,设计了一种促销活动.在一个不透明的箱子里放有4个完全相同的小球,球上分别标有“0元”、“10元”、“30元”和“50元”的字样.规定:顾客在本商场同一日内,消费每满300元,就可以从箱子里先后摸出两个球(每次只摸出一个球,第一次摸出后不放回).商场根据两个小球所标金额之和返还相应价格的购物券,可以重新在本商场消费.某顾客消费刚好满300元,则在本次消费中:
(1)该顾客至少可得___元购物券,至多可得___元购物券;
(2)请用画树状图或列表法,求出该顾客所获购物券的金额不低于50元的概率.
【答案】(1)10,80(2)![]()
【解析】解:(1)10,80。
(2)列表得:
0 | 10 | 30 | 50 | |
0 | - | (0,10) | (0,30) | (0,50) |
10 | (10,0) | - | (10,30) | (10,50) |
30 | (30,0) | (30,10) | - | (30,50) |
50 | (50,0) | (50,10) | (50,30) | - |
∵两次摸球可能出现的结果共有12种,每种结果出现的可能性相同,而所获购物券的金额不低于50元的结果共有6种。
∴该顾客所获购物券的金额不低于50元的概率是:![]() 。
。
(1)根据题意即可求得该顾客至少可得的购物券,至多可得的购物券的金额。
根据题意得:该顾客至少可得购物券:0+10=10(元),至多可得购物券:30+50=80(元)。
(2)首先根据题意列出表格或画树状图,然后由图表求得所有等可能的结果与该顾客所获购物券的金额不低于50元的情况,再利用概率公式求解即可求得答案。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校随机抽取九年级部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,学校收集整理数据后,将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题:
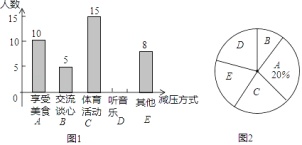
![]() 九年级接受调查的同学共有多少名,并补全条形统计图;
九年级接受调查的同学共有多少名,并补全条形统计图;
![]() 九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;
九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;
![]() 若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.
若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下短文,然后解决下列问题:
如果一个三角形和一个矩形满足条件:三角形的一边与矩形的一边重合,且三角形的这边所对的顶点在矩形这边的对边上,则称这样的矩形为三角形的“友好矩形”. 如图①所示,矩形ABEF即为△ABC的“友好矩形”. 显然,当△ABC是钝角三角形时,其“友好矩形”只有一个 .
(1) 仿照以上叙述,说明什么是一个三角形的“友好平行四边形”;
(2) 如图②,若△ABC为直角三角形,且∠C=90°,在图②中画出△ABC的所有“友好矩形”,并比较这些矩形面积的大小;
(3) 若△ABC是锐角三角形,且BC>AC>AB,在图③中画出△ABC的所有“友好矩形”,指出其中周长最小的矩形并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象分别与x轴、y轴交于点A、C,与反比列函数
的图象分别与x轴、y轴交于点A、C,与反比列函数![]() 的图象在第一象限内交于点P,过点P作
的图象在第一象限内交于点P,过点P作![]() 轴,垂足为B,且
轴,垂足为B,且![]() 的面积为9.
的面积为9.
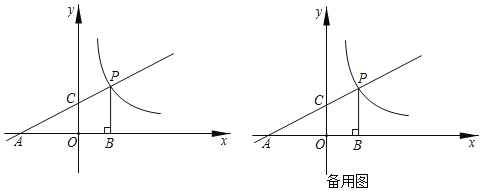
![]() 点A的坐标为______,点C的坐标为______,点P的坐标为______;
点A的坐标为______,点C的坐标为______,点P的坐标为______;
![]() 已知点Q在反比例函数
已知点Q在反比例函数![]() 的图象上,其横坐标为6,在x轴上确定一点M,使得
的图象上,其横坐标为6,在x轴上确定一点M,使得![]() 的周长最小,求出点M的坐标;
的周长最小,求出点M的坐标;
![]() 设点E是反比例函数
设点E是反比例函数![]() 在第一象限内图象上的一动点,且点E在直线PB的右侧,过点E作
在第一象限内图象上的一动点,且点E在直线PB的右侧,过点E作![]() 轴,垂足为F,当
轴,垂足为F,当![]() 和
和![]() 相似时,求动点E的坐标.
相似时,求动点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
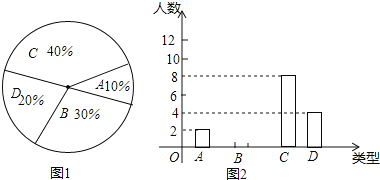
【题目】某校要求200名学生进行社会调查,每人必须完成![]() 份报告,调查结束后随机抽查了20名学生每人完成报告的份数,并分为四类,A:3份;B:4份;C:5份;D:6份,将各类的人数绘制成扇形图
份报告,调查结束后随机抽查了20名学生每人完成报告的份数,并分为四类,A:3份;B:4份;C:5份;D:6份,将各类的人数绘制成扇形图![]() 如图
如图![]() 和尚未完整的条形图
和尚未完整的条形图![]() 如图
如图![]() ,回答下列问题:
,回答下列问题:
![]() 请将条形统计图2补充完整;
请将条形统计图2补充完整;
![]() 写出这20名学生每天完成报告份数的众数______份和中位数______份;
写出这20名学生每天完成报告份数的众数______份和中位数______份;
![]() 在求出20名学生每人完成报告份数的平均数时,小明是这样分析的:
在求出20名学生每人完成报告份数的平均数时,小明是这样分析的:
第一步:求平均数的公式是![]() ;
;
第二步:在该问题中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
第三步:![]() (份);
(份);
小明的分析对不对?如果对,请说明理由,如果不对,请求出正确结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
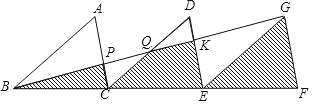
【题目】如图,已知△ABC≌△DCE≌△GEF,三条对应边BC.CE、EF在同一条直线上,连接BG,分别交AC、DC、DE于点P、Q、K,其中S△PQC=3,则图中三个阴影部分的面积和为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为庆祝国庆节举办游园活动,小军来到摸球兑奖活动场地,李老师对小军说:“这里有甲、乙两个盒子,里面都装有一些乒乓球,你只能选择在其中一个盒子中摸球。”获奖规则如下:
甲盒中有白色乒乓球4个,黄色乒乓球1个,一人只能摸一次且一次摸出一个球,若这个球为黄色球,则可获得玩具熊一个,否则不得奖;
乙盒中有白色乒乓球2个,黄色乒乓球3个,一人只能摸一次且一次摸出两个球,若这两个球均为黄色球,则可获得玩具熊一个,否则不得奖;
请问小军在哪个盒子内摸球获得玩具熊的机会更大?请用概率知识说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com