
【题目】阅读以下短文,然后解决下列问题:
如果一个三角形和一个矩形满足条件:三角形的一边与矩形的一边重合,且三角形的这边所对的顶点在矩形这边的对边上,则称这样的矩形为三角形的“友好矩形”. 如图①所示,矩形ABEF即为△ABC的“友好矩形”. 显然,当△ABC是钝角三角形时,其“友好矩形”只有一个 .
(1) 仿照以上叙述,说明什么是一个三角形的“友好平行四边形”;
(2) 如图②,若△ABC为直角三角形,且∠C=90°,在图②中画出△ABC的所有“友好矩形”,并比较这些矩形面积的大小;
(3) 若△ABC是锐角三角形,且BC>AC>AB,在图③中画出△ABC的所有“友好矩形”,指出其中周长最小的矩形并加以证明.

【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】
(1)类似“友好矩形”的定义,即可写出“友好平行四边形”的定义:如果一个三角形和一个平行四边形满足条件:三角形的一边与平行四边形的一边重合,三角形这边所对的顶点在平行四边形这边的对边上,则称这样的平行四边形为三角形的“友好平行四边形”;
(2)根据定义,则分别让直角三角形的直角边或斜边当矩形的一边,过第三个顶点作它的对边,从而画出矩形.根据每个矩形和直角三角形的面积的关系,比较两个矩形的面积大小;
(3)分别以三角形的一边当矩形的另一边,过第三个顶点作矩形的对边,从而画出矩形,根据三角形和矩形的面积公式,可知三个矩形的面积相等,设矩形的面积是S,三角形的三条边分别是a,b,c.根据矩形的面积由其中一边表示出矩形的另一边,进一步求得其周长,运用求差法比较它们的周长的大小.
(1) 如果一个三角形和一个平行四边形满足条件:三角形的一边与平行四边形的一边重合,三角形这边所对的顶点在平行四边形这边的对边上,则称这样的平行四边形为三角形的“友好平行四边形”.
(2) 此时共有2个友好矩形,如图的矩形BCAD、矩形ABEF.
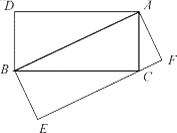
易知,矩形BCAD、ABEF的面积都等于△ABC面积的2倍,∴ △ABC的“友好矩形”的面积相等.
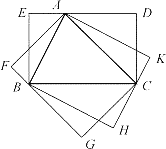
(3) 此时共有3个友好矩形,如图的BCDE、CAFG及ABHK,其中的矩形ABHK的周长最小 .
证明如下:易知,这三个矩形的面积相等,令其为S. 设矩形BCDE、CAFG及ABHK的周长分别为L1,L2,L3,△ABC的边长BC=a,CA=b,AB=c,则L1=![]() +2a,L2=
+2a,L2=![]() +2b,L3=
+2b,L3=![]() +2c .
+2c .
∴ L1- L2=(![]() +2a)-(
+2a)-(![]() +2b)=2(a-b)
+2b)=2(a-b)![]() ,而 ab>S,a>b,
,而 ab>S,a>b,
∴ L1- L2>0,即L1> L2 . 同理可得,L2> L3 .
∴ L3最小,即矩形ABHK的周长最小.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
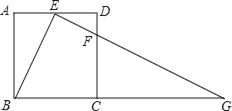
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF:DC=1:4,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为10,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
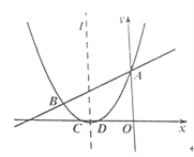
【题目】如图,抛物线 y=![]() x+bx+c 与直线 y=
x+bx+c 与直线 y= ![]() x+3 交于 A,B 两点,点 A 在 y 轴上,抛物线交 x 轴于 C、D 两点,已知 C(-3,0).
x+3 交于 A,B 两点,点 A 在 y 轴上,抛物线交 x 轴于 C、D 两点,已知 C(-3,0).
(1)求抛物线的解析式
(2)在抛物线对称轴 l 上找一点 M,使|MB 一 MD|的值最大。请求出点 M 的坐标及这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙.
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子,并用线段表示;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:制作无盖盒子
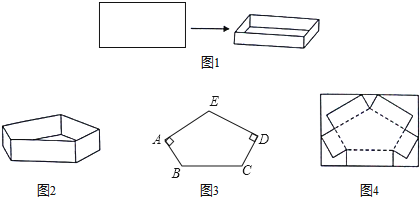
任务一:如图1,有一块矩形纸板,长是宽的2倍,要将其四角各剪去一个正方形,折成高为4cm,容积为![]() 的无盖长方体盒子
的无盖长方体盒子![]() 纸板厚度忽略不计
纸板厚度忽略不计![]() .
.
![]() 请在图1的矩形纸板中画出示意图,用实线表示剪切线,虚线表示折痕.
请在图1的矩形纸板中画出示意图,用实线表示剪切线,虚线表示折痕.
![]() 请求出这块矩形纸板的长和宽.
请求出这块矩形纸板的长和宽.
任务二:图2是一个高为4cm的无盖的五棱柱盒子![]() 直棱柱
直棱柱![]() ,图3是其底面,在五边形ABCDE中,
,图3是其底面,在五边形ABCDE中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 试判断图3中AE与DE的数量关系,并加以证明.
试判断图3中AE与DE的数量关系,并加以证明.
![]() 图2中的五棱柱盒子可按图4所示的示意图,将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少各为多少cm?请直接写出结果
图2中的五棱柱盒子可按图4所示的示意图,将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少各为多少cm?请直接写出结果![]() 图中实线表示剪切线,虚线表示折痕
图中实线表示剪切线,虚线表示折痕![]() 纸板厚度及剪切接缝处损耗忽略不计
纸板厚度及剪切接缝处损耗忽略不计![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动.在一个不透明的箱子里放有4个完全相同的小球,球上分别标有“0元”、“10元”、“30元”和“50元”的字样.规定:顾客在本商场同一日内,消费每满300元,就可以从箱子里先后摸出两个球(每次只摸出一个球,第一次摸出后不放回).商场根据两个小球所标金额之和返还相应价格的购物券,可以重新在本商场消费.某顾客消费刚好满300元,则在本次消费中:
(1)该顾客至少可得___元购物券,至多可得___元购物券;
(2)请用画树状图或列表法,求出该顾客所获购物券的金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考前,某校文具店以每套5元购进若干套考试用具,为让利考生,该店决定售价不超过7元,在几天的销售中发现每天的销售数量y(套)和售价x(元)之间存在一次函数关系,绘制图象如图.
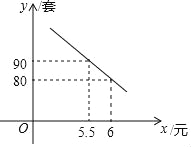
(1)y与x的函数关系式为 (并写出x的取值范围);
(2)若该文具店每天要获得利润80元,则该套文具的售价为多少元?
(3)设销售该套文具每天获利w元,则销售单价应为多少元时,才能使文具店每天的获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2个,黄球有1个,蓝球有1个.现有一张电影票,小明和小亮决定通过摸球游戏定输赢(赢的一方得电影票).游戏规则是:两人各摸1次球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,将小球摇匀,再由小亮随机摸出1个球并记录颜色.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你利用树状图或列表法说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com