
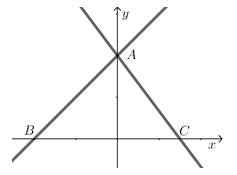
【题目】如图,在平面直角坐标系中,直线y=x+4与y轴交于点A,与x轴交于点B,直线y=kx+b经过点A,且交x轴与点C(3,0).
(1)求直线AC的函数表达式;
(2)动点P在线段CB上由C向B匀速运动,到达点B后停止运动,运动速度为3个单位长度,过点P作PE⊥x轴,交直线AC于点E,过点E作直线GE∥x轴交![]() 轴于点F,交直线AB于点G,设点P的运动时间为t(t>0)秒.
轴于点F,交直线AB于点G,设点P的运动时间为t(t>0)秒.
①直接写出线段PE的长度(用含t的代数式表示);
②当EG=1时,请直接写出t的值.
【答案】(1)![]() ;(2)①4t;②
;(2)①4t;②![]() 或
或![]() .
.
【解析】
(1)根据直线AB的解析式y=x+4,求出点A的坐标,然后即可利用待定系数法求出直线AC的解析式;
(2)先根据已知条件求出点P坐标,点E和点P的横坐标相同,所以再将E点的横坐标代入AC解析式,即可求出PE的长;
(3)先根据现有条件表示出G点坐标,再分成当E点在第一象限和E点在第二象限两种情况讨论即可.
(1)∵点A在y=x+4上,
∴A的坐标为(0,4),
将A(0,4),C(3,0)代入AC的解析式y=kx+b,
得![]() ,
,
解得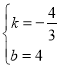 ,
,
∴AC的解析式为y=![]() x+4;
x+4;
(2)如图:

∵AB的解析式为y=x+4,
∴B的坐标为(-4,0),A的坐标为(0,4),
∴OB=4,OC=3,
∵CP=3t,
∴OP=OC-CP=3-3t,
∴P的坐标为(3-3t,0),
∵PE⊥x轴,
∴点E的横坐标为3-3t,
∵点E在y=![]() x+4上,
x+4上,
∴y=![]() (3-3t)+4=4t,
(3-3t)+4=4t,
∴PE的长为4t;
(3)∵GE∥x轴,
∴G的纵坐标为4t,
又∵G在y=x+4上,
∴4t=x+4,
解得x=4t-4,
∴G点的坐标为(4t-4,4t),
①如图,
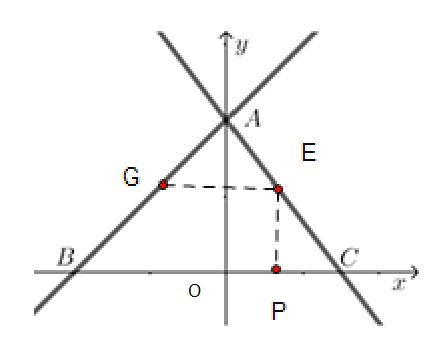
当E点在第一象限时,EG=3t-3-(4-4t)=1,
解得t=![]() ;
;
②如图,
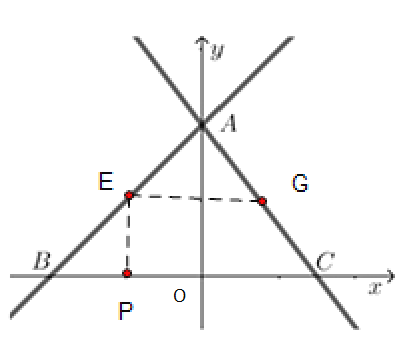
当E点在第二象限时,EG=3-3t-(4t-4)=1,
解得t=![]() ;
;
综上,t的值为![]() 或
或![]() .
.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】美丽的雪花扮靓了我们可爱的家乡,但高速公路清雪刻不容缓.某高速公路维护站引进甲、乙两种型号的清雪车,已知甲型清雪车比乙型清雪车每天多清理路段6千米,甲型清雪车清理90千米与乙型清雪车清理60千米路段所用的时间相同.
(1)甲型、乙型清雪车每天各清理路段多少千米?
(2)此公路维护站欲购置甲、乙两种型号清雪车共20台,甲型每台30万元,乙型每台15万元,若在购款不超过360万元,甲型、乙型都购买的情况下,甲型清雪车最多可购买几台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动.在一个不透明的箱子里放有4个完全相同的小球,球上分别标有“0元”、“10元”、“30元”和“50元”的字样.规定:顾客在本商场同一日内,消费每满300元,就可以从箱子里先后摸出两个球(每次只摸出一个球,第一次摸出后不放回).商场根据两个小球所标金额之和返还相应价格的购物券,可以重新在本商场消费.某顾客消费刚好满300元,则在本次消费中:
(1)该顾客至少可得___元购物券,至多可得___元购物券;
(2)请用画树状图或列表法,求出该顾客所获购物券的金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
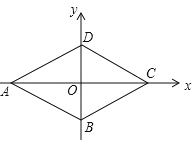
【题目】如图,已知菱形ABCD的顶点A(![]() ,0),∠DAB=60°,若动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,则第2020秒时,点P的坐标为____.
,0),∠DAB=60°,若动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,则第2020秒时,点P的坐标为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市以3元/本的价格购进某种笔记本若干,然后以5元/本的价格出售,每天售出20本.通过调查发现,这种笔记本的售价每降低0.1元,每天可多售出4本,为保证每天至少售出50本,该超市决定降价销售.
(1)若每本降价![]() 元,则每天的销售量是________本(用含
元,则每天的销售量是________本(用含![]() 的代数式表示).
的代数式表示).
(2)要想每天赢利60元,该超市需将每本的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图所示的两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
扇形统计图
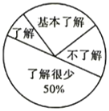
条形统计图

(1)接受问卷调查的学生共有_______人,扇形统计图中“不了解”部分所对应扇形的圆心角度数为_______,并把条形统计图补充完整;
(2)若该中学共有学生![]() 人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为_______人;
人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为_______人;
(3)若从对校园安全知识达到“了解”程度的![]() ,
,![]() ,
,![]()
![]() 个女生和
个女生和![]() ,
,![]()
![]() 个男生中随机抽取
个男生中随机抽取![]() 人参加校园安全知识竞赛,请用画树状图法或列表法求出恰好抽到
人参加校园安全知识竞赛,请用画树状图法或列表法求出恰好抽到![]() 个男生和
个男生和![]() 个女生的概率.
个女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com