Question

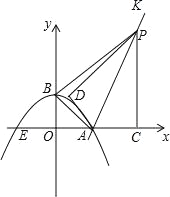
【题目】已知：如图，抛物线y=ax2+bx+2与x轴交于点A（4，0）、E（-2，0）两点，连结AB，过点A作直线AK⊥AB，动点P从A点出发以每秒个单位长度的速度沿射线AK运动，设运动时间为t秒，过点P作PC⊥x轴，垂足为C，把△ACP沿AP对折，使点C落在点D处．

（1）求抛物线的解析式；

（2）当点D在△ABP的内部时，△ABP与△ADP不重叠部分的面积为S，求S与t之间的函数关系式，并直接写出t的取值范围；

（3）若线段AC的长是线段BP长的，请直接写出此时t的值；

（4）是否存在这样的时刻，使动点D到点O的距离最小？若存在请直接写出这个最小距离；若不存在，说明理由．

Answer 1

【答案】（1）y=-x2+x+2，（2）S=-t2+5t（0＜t＜4）（3）t=；（4）.

【解析】

试题分析：（1）用待定系数法求出抛物线解析式；

（2）先根据点D在△APB内部，求出t的范围，然后用△APB减去△APC面积求出不重叠的部分面积；

（3）根据两点间的距离公式表示出BP，根据条件建立方程，求出时间；

（4）先判断出点D到点O的距离最小时的位置，然后用三角函数和勾股定理计算．

试题解析：（1）将A，B，E三点代入抛物线解析式中，得

，∴

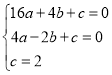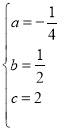
∴y=-x2+x+2，

（2）∵A（4，0），B（0，2）

∴直线AB解析式为y=-x+2，

∵AB⊥AK，

∴直线AK解析式为y=2x+8，

∴tan∠PAC==2，

∵AP=t，

∴AC=t，PC=2t，

∵D在△ABP内部，

∴∠APB＞∠APC，

∴tan∠APB＞tan∠APC，

∴，

∴，

∴t＜4，

∴0＜t＜4，

∴S=S△APB-S△APD

=S△APB-S△APC

=×AB×AP-×AC×PC

=×2×t-×t×2t

=-t2+5t（0＜t＜4）

（3）∵P（t+4，2t），

∴BP=，

∵线段AC的长是线段BP长的，

∴t=，

∴t=-（舍）t=

（4）要使点D到O的距离最小，则有点D在OP上，此时记作D1

在Rt△OCP中，tan∠POC=，

在Rt△OCP中，tan∠AOC=，

∴，

∴OD1=，

根据勾股定理得，OD12+AD12=OA2，

∴（）2+t2=16，

∴t=-4（舍）t=，

∴AD1==.