
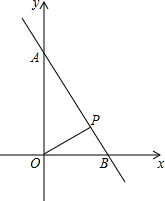
 如图,在平面直角坐标系中.已知点A(0,1+$\sqrt{3}$)和B(1+$\sqrt{3}$,0),点P在线段AB上,∠BOP=30°.
如图,在平面直角坐标系中.已知点A(0,1+$\sqrt{3}$)和B(1+$\sqrt{3}$,0),点P在线段AB上,∠BOP=30°.分析 (1)由OA=OB,则△POB绕点O逆时针旋转90°后B点的对应点为A,再利用P′O=PO,且∠POP′=90°可画出P′点,则△P′OA为所求;
(2)作PH⊥x轴于H,P′H′⊥y轴于H′,先判断△OAB为等腰直角三角形得到∠OBA=45°,设PH=a,则NH=a,在Rt△POH中利用含30度的直角三角形三边的关系得到OH=$\sqrt{3}$PH=$\sqrt{3}$a,$\sqrt{3}$a+a=1+$\sqrt{3}$,解得a=1,所以OH=$\sqrt{3}$,PH=1,然后根据旋转的性质得P′H=PH=1,OH′=OH=$\sqrt{3}$,所以P′的坐标为(-1,$\sqrt{3}$);
(3)先计算出OP=2PH=2,然后根据扇形面积公式求解.
解答 解:(1)如图,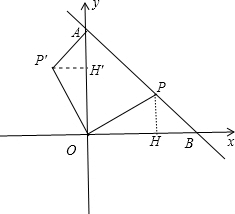 △P′OA为所作;
△P′OA为所作;
(2)作PH⊥x轴于H,P′H′⊥y轴于H′,
∵A(0,1+$\sqrt{3}$)和B(1+$\sqrt{3}$,0),
∴OA=OB=1+$\sqrt{3}$,
∴△OAB为等腰直角三角形,
∴∠OBA=45°,
设PH=a,则NH=a,
在Rt△POH中,∵∠HOP=30°,
∴OH=$\sqrt{3}$PH=$\sqrt{3}$a,
∴$\sqrt{3}$a+a=1+$\sqrt{3}$,解得a=1,
∴OH=$\sqrt{3}$,PH=1,
∵△POB绕点O逆时针旋转90°得到△P′OA,
∴P′H=PH=1,OH′=OH=$\sqrt{3}$,
∴旋转变换后点P的对应点P′的坐标为(-1,$\sqrt{3}$);
(3)OP=2PH=2,
旋转过程中线段OP扫过的面积=$\frac{90π•{2}^{2}}{360}$=π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 家电名称 | 电饭煲 | 洗衣机 | 热水器 |
| 使用时间段 | 8:00~8:20 | 21:05~21:45 | 20:45~21:20 |
| 用电量/kW•h | 0.4 | 0.6 | 3.5 |
| 电费/元 | 0.22 | 0.18 | 1.425 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
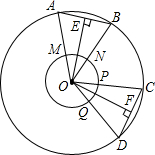 如图所示.两个同心圆⊙O,点A、B、C、D在外圆上,点M、N、P、Q在内圆上,0E是AB的弦心距,OF平分∠COD,且$\widehat{MN}$=$\widehat{PQ}$,求证:OE=OF.
如图所示.两个同心圆⊙O,点A、B、C、D在外圆上,点M、N、P、Q在内圆上,0E是AB的弦心距,OF平分∠COD,且$\widehat{MN}$=$\widehat{PQ}$,求证:OE=OF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
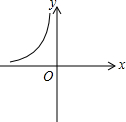 如图是反比例函数y=$\frac{n+7}{x}$的图象的一支,根据图象回答下列问题
如图是反比例函数y=$\frac{n+7}{x}$的图象的一支,根据图象回答下列问题查看答案和解析>>
科目:初中数学 来源: 题型:填空题
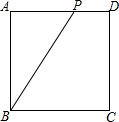 如图所示,正方形ABCD的边长为4cm,点P是AD边上的一个动点,则△ABP的面积S(cm2)与AP的长x(cm)之间的函数表达式为S=2x,x的取值范围是0<x<4.
如图所示,正方形ABCD的边长为4cm,点P是AD边上的一个动点,则△ABP的面积S(cm2)与AP的长x(cm)之间的函数表达式为S=2x,x的取值范围是0<x<4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
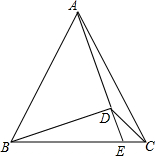 在△ABC中,AB=AC,以AB为斜边构成等腰Rt△ABD,∠ADB=90°,延长AD交BC于E,连接CD,∠DCB=45°.若S△ABE=15,CE=1,则AB=3$\sqrt{5}$.
在△ABC中,AB=AC,以AB为斜边构成等腰Rt△ABD,∠ADB=90°,延长AD交BC于E,连接CD,∠DCB=45°.若S△ABE=15,CE=1,则AB=3$\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com