
【题目】根据如图所示的数轴,解答下面问题.

(1)分别写出![]() 、
、![]() 两点所表示的有理数;
两点所表示的有理数;
(2)请问![]() 、
、![]() 两点之间的距离是多少?
两点之间的距离是多少?
(3)在数轴上画出与![]() 点距离为2的点(用不同于
点距离为2的点(用不同于![]() 、
、![]() 的其它字母表).
的其它字母表).
【答案】(1)点![]() 表示1;点
表示1;点![]() 表示-2.5;(2)距离是3.5;(3)两点C、D分别是-1,3,图详见解析.
表示-2.5;(2)距离是3.5;(3)两点C、D分别是-1,3,图详见解析.
【解析】
(1)观察数轴,即可找出A、B两点表示的数;
(2)根据两点的距离公式,即可求出A、B两点之间的距离;
(3)设与A点距离为2的点表示的数为x,根据两点间的距离公式即可得出关于x的含绝对值符号的一元一次方程,解之即可得出x的值,将其标记在数轴上即可.
解:(1)根据数轴可知点![]() 表示1;点
表示1;点![]() 表示-2.5;
表示-2.5;
(2)依题意得:AB之间的距离为:![]() =1+2.5=3.5;
=1+2.5=3.5;
(3)设与A点距离为2的点表示的数为x,
根据题意得:|x-1|=2,
解得:x=-1或x=3.
将其标记在数轴上,点C、D即为所求.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
A.放下自我,彼此尊重; B.放下利益,彼此平衡;
C.放下性格,彼此成就; D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟.根据同学们的选择情况,小明绘制了下面两幅不完整的图表,请根据图表中提供的信息,解答下列问题:

(1)参加本次讨论的学生共有 人;
(2)表中![]() ,
,![]() ;
;
(3)将条形统计图补充完整;
(4)现准备从![]() 四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点
四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点![]() (合理竞争,合作双赢)的概率.
(合理竞争,合作双赢)的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们的平均亩产量分别是![]() =610千克,
=610千克, ![]() =609千克,亩产量的方差分别是
=609千克,亩产量的方差分别是![]() =29.6,
=29.6, ![]() =2.则关于两种小麦推广种植的合理决策是( )
=2.则关于两种小麦推广种植的合理决策是( )
A. 甲的平均亩产量较高,应推广甲
B. 甲、乙的平均亩产量相差不多,均可推广
C. 甲的平均亩产量较高,且亩产量比较稳定,应推广甲
D. 甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙
查看答案和解析>>
科目:初中数学 来源: 题型:
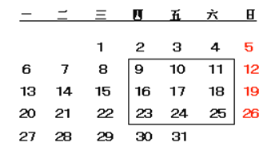
【题目】如图:是某月份的月历表,请你认真观察月历表,回答以下问题:
(1)如果圈出同一行的三个数,用a表示中间的数,则第一个数,第三个数怎样表示?
(2)如果圈出同一列的三个数,用a表示中间的数,则第一个数,第三个数怎样表示?
(3)如果圈出如图所示的任意9个数,这9个数的和可能是207吗?如果可能,请求出这9个数;如果不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 中,
中,![]() 是
是![]() 边上一点,
边上一点,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 的延长线于
的延长线于![]() ,且
,且![]() ,连接
,连接![]() .
.
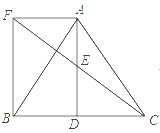
(1)求证:![]() 是
是![]() 的中点;
的中点;
(2)若![]() ,试判断四边形
,试判断四边形![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
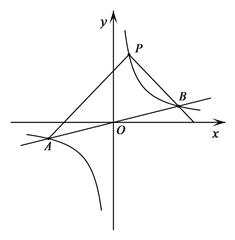
【题目】如图,反比例函数y=![]() 的图象与一次函数y=
的图象与一次函数y=![]() x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
(1)若点P的坐标是(1,4),直接写出k的值和△PAB的面积;
(2)设直线PA、PB与x轴分别交于点M、N,求证:△PMN是等腰三角形;
(3)设点Q是反比例函数图象上位于P、B之间的动点(与点P、B不重合),连接AQ、BQ,比较∠PAQ与∠PBQ的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
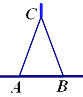
【题目】小知识:如图,我们称两臂长度相等(即![]() )的圆规为等臂圆规. 当等臂圆规的两脚摆放在一条直线上时,若张角
)的圆规为等臂圆规. 当等臂圆规的两脚摆放在一条直线上时,若张角![]() ,则底角
,则底角![]() .
.
请运用上述知识解决问题:
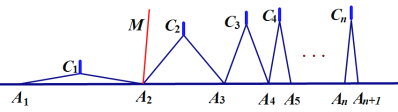
如图,![]() 个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
![]() ,
,![]() ,
, ![]() ,
,![]() ,…
,…
(1)、①由题意可得![]() = ;
= ;
②若![]() 平分
平分![]() ,则
,则![]() = ;
= ;
(2)、![]() = (用含
= (用含![]() 的代数式表示);
的代数式表示);
(3)、当![]() 时,设
时,设![]() 的度数为
的度数为![]() ,
,![]() 的角平分线
的角平分线![]() 与
与![]() 构成的角的度数为
构成的角的度数为![]() ,那么
,那么![]() 与
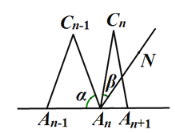
与![]() 之间的等量关系是 ,请说明理由. (提示:可以借助下面的局部示意图)
之间的等量关系是 ,请说明理由. (提示:可以借助下面的局部示意图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com