
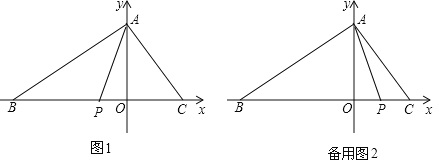
【题目】如图,在平面直角坐标系中,O为坐标原点.△ABC的边BC在x轴上,A、C两点的坐标分别为A(0,m)、C(n,0),B(﹣5,0),且![]() ,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.
,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.
(1)求A、C两点的坐标;
(2)连接PA,用含t的代数式表示△POA的面积;
(3)当P在线段BO上运动时,是否存在一点P,使△PAC是等腰三角形?若存在,请写出满足条件的所有P点的坐标并求t的值;若不存在,请说明理由。

【答案】(1)A的坐标是![]() ,
,![]() 的坐标是
的坐标是![]() ;(2)当
;(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;(3)存在一点
;(3)存在一点![]() 、
、![]() 、
、![]() ,
,![]() 相对应的时间分别是
相对应的时间分别是![]() 、1.5、
、1.5、![]() 使
使![]() 是等腰三角形.
是等腰三角形.
【解析】
(1)根据偶次方和算术平方根的非负性得出![]() ,
,![]() ,求出即可;
,求出即可;
(2)分为三种情况:当![]() 时,
时,![]() 在线段
在线段![]() 上,②当
上,②当![]() 时,
时,![]() 和
和![]() 重合,③当
重合,③当![]() 时,
时,![]() 在射线
在射线![]() 上,求出
上,求出![]() 和
和![]() ,根据三角形的面积公式求出即可;
,根据三角形的面积公式求出即可;
(3)分为三种情况:①![]() 为顶角时,找出腰长关系便可解;②
为顶角时,找出腰长关系便可解;②![]() 为顶角时,找出腰长关系便可解;③
为顶角时,找出腰长关系便可解;③![]() 为顶角时,根据勾股定理可求得.
为顶角时,根据勾股定理可求得.
解:(1)![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 的坐标是
的坐标是![]() ,
,![]() 的坐标是
的坐标是![]() ;
;
(2)![]() ,
,
![]() ,
,
①当![]() 时,
时,![]() 在线段
在线段![]() 上,如图1,
上,如图1,
![]() ,
,![]() ,
,
![]() 的面积
的面积![]() ;
;
②当![]() 时,
时,![]() 和
和![]() 重合,此时
重合,此时![]() 不存在,即
不存在,即![]() ;
;
③当![]() 时,
时,![]() 在射线
在射线![]() 上,如备用图2,
上,如备用图2,
![]() ,
,![]() ,
,
![]() 的面积
的面积![]() ;
;
(3)![]() 在线段
在线段![]() 上运动使
上运动使![]() 是等腰三角形,分三种情况,
是等腰三角形,分三种情况,
①![]() 为顶角时,即
为顶角时,即![]() ,
,
![]() 为
为![]() 中垂线,
中垂线,
![]() ,
,
![]() 点坐标为
点坐标为![]() ,
,![]() .
.
![]() ;
;
②![]() 为顶角时,
为顶角时,![]()
根据勾股定理可得,![]() ,
,
∵P在OB上,
![]() 点坐标为
点坐标为![]() ,
,![]()
![]() ;
;
③![]() 为顶角时,
为顶角时,![]() ,设
,设![]() ,
,
根据勾股定理,在![]() 中,
中,![]()
解得![]() ,
,
![]() ,
,
![]() 点坐标为
点坐标为![]() ,
,![]() ,
,![]() ,
,
![]() ;
;
综上,存在一点![]() 、
、![]() 、
、![]() ,
,![]() 相对应的时间分别是
相对应的时间分别是![]() 、1.5、
、1.5、![]() 使
使![]() 是等腰三角形.
是等腰三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图①,△ABC为等腰直角三角形, △ABD为等边三角形,连接CD.
(1)求∠ACD的度数;
(2)如图①,作∠BAC的平分线交CD于点E,求证:DE=AE+CE;
(3)如图②,在(2)的条件下,M为线段BC右侧一点,满足∠CMB=60°,求证:ME平分∠CMB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内的两条直线有相交和平行两种位置关系。
(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD +∠D,得∠BPD=∠B-∠D。将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;



(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系? (不需证明);
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数。

![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了10m到达D处,此时遇到一斜坡,坡度i=1:![]() ,沿着斜坡前进10米到达E处测得建筑物顶部的仰角是45°,请求出该建筑物BC的高度为( )(结果可带根号)
,沿着斜坡前进10米到达E处测得建筑物顶部的仰角是45°,请求出该建筑物BC的高度为( )(结果可带根号)

A. 5![]() +5 B. 5
+5 B. 5![]() +5 C. 5
+5 C. 5![]() +10 D. 5
+10 D. 5![]() +10
+10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,每旋转60°为滚动1次,那么当正六边形ABCDEF滚动2017次时,点F的坐标是( )

A. (2017,0) B. (2017![]() ,
, ![]() ) C. (2018,
) C. (2018, ![]() ) D. (2018,0)
) D. (2018,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠C=90°,AD平分∠BAC,DE⊥AB于点E,有下列结论:①CD=ED ;②AC+ BE= AB ;③DA平分∠CDE ;④∠BDE =∠BAC;⑤![]() =AB:AC.其中结论正确的个数有()
=AB:AC.其中结论正确的个数有()
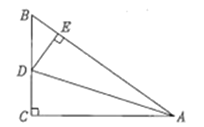
A.5个B.4个
C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACB=90,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D、E.
(1)求证:△ACD≌△CBE;
(2)已知AD=5,DE=3,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
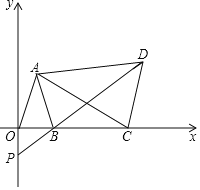
【题目】如图,在xOy中,已知点A(a﹣1,a+b),B(a,0),且![]() =0,C为x轴上B点右侧的动点,以AC为腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,DB交y轴于点P.
=0,C为x轴上B点右侧的动点,以AC为腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,DB交y轴于点P.
(1)求A、B两点坐标;
(2)求证:AO=AB;
(3)求证:∠OBP=∠OAB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com