
【题目】如图,∠ACB=90,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D、E.
(1)求证:△ACD≌△CBE;
(2)已知AD=5,DE=3,求BE的长.

【答案】(1)详见解析;(2)2.
【解析】
(1)根据垂直定义求出∠BEC=∠ACB=∠ADC,根据等式性质求出∠ACD=∠CBE,根据AAS证明△BCE≌△CAD;
(2)根据全等三角形的对应边相等得到AD=CE,CD=BE,再根据AD=5,DE=3,即可解答.
(1)证明:∵∠ACB=90°,BE⊥CE,
∴∠ECB+∠ACD=90°∠ECB+∠CBE=90°,
∴∠ACD=∠CBE,
∵AD⊥CE,BE⊥CE,
∴∠ADC=∠CEB=90°,
在△ACD和△CBE中, ,
,
∴△ACD≌△CBE(AAS);
(2)解:∵△ACD≌△CBE,
∴AD=CE=5,CD=BE,
∴BE=CD=CE﹣DE=5-3=2.


科目:初中数学 来源: 题型:
【题目】在世界经济的影响下,国家采取扩大内需的政策,基建投资成为拉动内需最强有力的引擎,金强公司中标一项工程,在甲、乙两地施工,其中甲地需推土机30台,乙地需推土机26台,公司在A、B两地分别库存推土机32台和24台,现从A地运一台到甲、乙两地的费用分别是400元和300元.从B地运一台到甲、乙两地的费用分别为200元和500元,设从A地运往甲地x台推土机,运这批推土机的总费用为y元.
(1)根据题意,可将库存地和施工地之间推土机的运输数量列表如下:
甲地(台) | 乙地(台) | 合计 | |
A地 | x | A地库存:32 (台) | |
B地 | B地库存:24 (台) | ||
合计 | 甲地需求:30 (台) | 乙地需求:26 (台) | 总计:56 (台) |
(2)求y与x的函数关系式;
(3)当x取何值时,能使运送这批推土机的总费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点.△ABC的边BC在x轴上,A、C两点的坐标分别为A(0,m)、C(n,0),B(﹣5,0),且![]() ,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.
,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.
(1)求A、C两点的坐标;
(2)连接PA,用含t的代数式表示△POA的面积;
(3)当P在线段BO上运动时,是否存在一点P,使△PAC是等腰三角形?若存在,请写出满足条件的所有P点的坐标并求t的值;若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
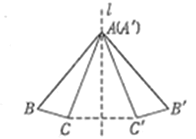
【题目】如图,△ABC和△A'B'C'关于直线l对称,下列结论:①△ABC≌△A'B'C' ;②∠BAC=∠B'A'C';③直线l不一定垂直平分线段CC';④直线BC与B'C'的交点一定在直线l上.其中正确的是________ (填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若DE=5,BD=3,则线段CE的长为( )

A. 3 B. 1 C. 2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,AB=10,AD=8,将纸片折叠,使点B落在CD上的B′处,折痕为AE,在折痕AE上存在一点P到边CD的距离与到点B的距离相等,则此相等的距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过
经过![]() ,
,![]() 两点.
两点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在
在![]() 上方的抛物线上有一动点
上方的抛物线上有一动点![]() .
.
①如图![]() ,当点
,当点![]() 运动到某位置时,以
运动到某位置时,以![]() ,
,![]() 为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点
为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点![]() 的坐标;
的坐标;
②如图![]() ,过点
,过点![]() ,
,![]() 的直线
的直线![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() (k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线
(k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线![]() (k>0)上一点,且在第一象限内,若△AOC的面积为6.
(k>0)上一点,且在第一象限内,若△AOC的面积为6.
(1)求双曲线的解析式;
(2)求点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),
C(3,4)
⑴ 作出与△ABC关于y轴对称△A1B1C1,并写出 三个顶点的坐标为:A1( ),B1( ),C1( );
⑵ 在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标;
⑶ 在 y 轴上是否存在点 Q,使得S△AOQ=![]() S△ABC,如果存在,求出点 Q 的坐标,如果不存在,说明理由。
S△ABC,如果存在,求出点 Q 的坐标,如果不存在,说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com