
【题目】在世界经济的影响下,国家采取扩大内需的政策,基建投资成为拉动内需最强有力的引擎,金强公司中标一项工程,在甲、乙两地施工,其中甲地需推土机30台,乙地需推土机26台,公司在A、B两地分别库存推土机32台和24台,现从A地运一台到甲、乙两地的费用分别是400元和300元.从B地运一台到甲、乙两地的费用分别为200元和500元,设从A地运往甲地x台推土机,运这批推土机的总费用为y元.
(1)根据题意,可将库存地和施工地之间推土机的运输数量列表如下:
甲地(台) | 乙地(台) | 合计 | |
A地 | x | A地库存:32 (台) | |
B地 | B地库存:24 (台) | ||
合计 | 甲地需求:30 (台) | 乙地需求:26 (台) | 总计:56 (台) |
(2)求y与x的函数关系式;
(3)当x取何值时,能使运送这批推土机的总费用最少?
【答案】(1)见解析;(2)y=400x+12600;(3)当x=6时,总费用最小
【解析】
(1)设从A地运往甲地x台,从A地运往乙地的推土机(32x)台,从B地运往甲地的推土机(30x),运往乙地的推土机(x6)台,
(2)根据现从A地运一台到甲、乙两地的费用分别是400元和300元.从B地运一台到甲、乙两地的费用分别为200元和500元,可求出运这批推土机的总费用.
(2)根据函数的性质可判断费用何时最少.
解:(1) 根据题意,可将库存地和施工地之间推土机的运输数量列表如下:
甲地 | 乙地 | 合计 | |
A地 | x (台) | 32-x (台) | A地库存:32 (台) |
B地 | 30-x (台) | 26-(32-x)=24-(30-x)=x-6 (台) | B地库存:24 (台) |
合计 | 甲地需求:30 (台) | 乙地需求:26 (台) | 总计:56 (台) |
(2)从A地往甲地运推土机的费用为:400x,
从A地往乙地运推土机的费用为:300(32-x),
从B地往甲地运推土机的费用为:200(30-x),
从B地往乙地运推土机的费用为:500[26-(32-x)].
故运甲、乙两地所需的这批推土机的总费用y可以表示为:
y=400x+300(32-x)+200(30-x)+500[26-(32-x)]=400x+12600,
即y=400x+12600.
(2) 由于各地之间的运输数量均与x的取值有关. 从实际情况来看,x的取值必须保证各地之间的运输数量均为非负数. 因此,x的取值必须满足:
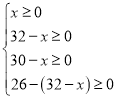 ,
,
解此不等式组,得
6≤x≤30.
由运送这批推土机的总费用y和从A地运往甲地的推土机的数量x的关系y=400x+12600可知,y与x满足一次函数关系,且y随x的增大而增大. 故要使总费用y最小,则x应取最小值.
又因为x的取值范围为:6≤x≤30,所以当x=6时,总费用最小.


科目:初中数学 来源: 题型:
【题目】如图,在7×7网格中,每个小正方形的边长都为1.

(1)若点A(1,3),C(2,1), ①建立适当的平面直角坐标系;②点B的坐标为( , );
(2)判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC为等腰直角三角形, △ABD为等边三角形,连接CD.
(1)求∠ACD的度数;
(2)如图①,作∠BAC的平分线交CD于点E,求证:DE=AE+CE;
(3)如图②,在(2)的条件下,M为线段BC右侧一点,满足∠CMB=60°,求证:ME平分∠CMB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两个港口,水由A流向B,水流的速度是4千米/小时,甲、乙两船同时由A顺流驶向B,各自不停地在A、B之间往返航行,甲在静水中的速度是28千米/小时,乙在静水中的速度是20千米/小时.

设甲行驶的时间为t小时,甲船距B港口的距离为S1千米,乙船距B港口的距离为S2千米,如图为S1(千米)和t(小时)函数关系的部分图象.
(1)A、B两港口距离是_____千米.
(2)在图中画出乙船从出发到第一次返回A港口这段时间内,S2(千米)和t(小时)的函数关系的图象.
(3)求甲、乙两船第二次(不算开始时甲、乙在A处的那一次)相遇点M位于A、B港口的什么位置?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴打车为市民的出行带来了很大的方便,小亮调查了若干市民一周内使用滴滴打车的时间t(单位:分)
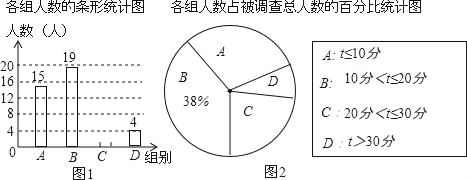
(1)这次被调查的总人数是多少?
(2)试求表示C组的扇形圆心角的度数,并补全条形统计图;
(3)若全市的总人数为666万,试求全市一周内使用滴滴打车超过20分钟的人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,等边三角形ABC的边长为5,点P在线段AB上,点D在线段BC上,且△PDE是等边三角形.
(1)初步尝试:若点P与点A重合时(如图1),BD+BE= .
(2)类比探究:将点P沿AB方向移动,使AP=1,其余条件不变(如图2),试计算BD+BE的值是多少?
(3)拓展迁移:如图3,在△ABC中,AB=AC,∠BAC=70°,点P在线段AB的延长线上,点D在线段CB的延长线上,在△PDE中,PD=PE,∠DPE=70°,设BP=a,请直接写出线段BD、BE之间的数量关系(用含a的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内的两条直线有相交和平行两种位置关系。
(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD +∠D,得∠BPD=∠B-∠D。将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;



(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系? (不需证明);
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数。

![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了10m到达D处,此时遇到一斜坡,坡度i=1:![]() ,沿着斜坡前进10米到达E处测得建筑物顶部的仰角是45°,请求出该建筑物BC的高度为( )(结果可带根号)
,沿着斜坡前进10米到达E处测得建筑物顶部的仰角是45°,请求出该建筑物BC的高度为( )(结果可带根号)

A. 5![]() +5 B. 5
+5 B. 5![]() +5 C. 5
+5 C. 5![]() +10 D. 5
+10 D. 5![]() +10
+10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACB=90,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D、E.
(1)求证:△ACD≌△CBE;
(2)已知AD=5,DE=3,求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com