
【题目】如图,已知函数y=x+2的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,4)且与x轴及y=x+2的图象分别交于点C、D,点D的坐标为(![]() ,n)
,n)
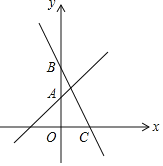
(1)则n= ,k= ,b=_______.
(2)若函数y=kx+b的函数值大于函数y=x+2的函数值,则x的取值范围是_______.
(3)求四边形AOCD的面积.
【答案】(1)![]() ,2,4;(2)x<
,2,4;(2)x<![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据点D在函数y=x+2的图象上,即可求出n的值;再利用待定系数法求出k,b的值;
(2)根据图象,直接判断即可;
(3)用三角形OBC的面积减去三角形ABD的面积即可.
(1)∵点D(![]() ,n)在直线y=x+2上,
,n)在直线y=x+2上,
∴n=![]() +2=
+2=![]() ,
,
∵一次函数经过点B(0,4)、点D(![]() ,
, ![]() ),
),
∴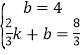 ,解得:
,解得:![]() ,
,
故答案为:![]() ,2,4;
,2,4;
(2)由图象可知,函数y=kx+b大于函数y=x+2时,图象在直线x=![]() 的左侧,
的左侧,
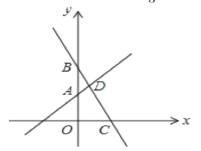
∴x<![]() ,
,
故答案为:x<![]() ,
,
(3)直线y=2x+4与x轴交于点C,
∴令y=0,得:2x+4=0,解得x=2,
∴点C的坐标为(2,0),
∵函数y=x+2的图象与y轴交于点A,
∴令x=0,得:y=2,
∴点A的坐标为(0,2),
S![]() =
=![]() ×2×4=4,
×2×4=4,
S![]() =
=![]() ×(42)×
×(42)×![]() =
=![]() ,
,
∴S![]() =S
=S![]() S
S![]() =4
=4![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】某天上午,一出租车司机始终在一条南北走向的笔直马路上营运,(出发点记作为点O,约定向南为正,向北为负),期间一共运载6名乘客,行车里程(单位:千米)依先后次序记录如下:﹢7,﹣3,﹢6,﹣1,﹢2,﹣4.
(1)出租车在行驶过程中,离出发点O最远的距离是______千米;
(2)将最后一名乘客送到目的地,出租车离出发点O多远?在O点的什么方向?
(3)出租车收费标准为:起步价(不超过3千米)为8元,超过3千米的部分每千米的价格为1.5元,求司机这天上午的营业额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:顺次连接矩形A1B1C1D1四边的中点得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点得四边形A3B3C3D3,…,按此规律得到四边形AnBnCnDn.若矩形A1B1C1D1的面积为24,那么四边形AnBnCnDn的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
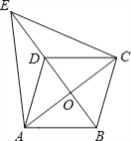
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若AC=8,AB=5,求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,在正方形 ABCD 中,E,F 分别是 AD,CD 上两点,BE 交 AF 于点 G,且 DE=CF.

(1)写出 BE 与 AF 之间的关系,并证明你的结论;
(2)如图 2,若 AB=2,点 E 为 AD 的中点,求 AG 的长度。
(3)在(2)的条件下,连接 GD,试证明 GD 是∠EGF 的角平分线,并求出 GD 的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2开始,连续的偶数相加,它们和的情况如下表:
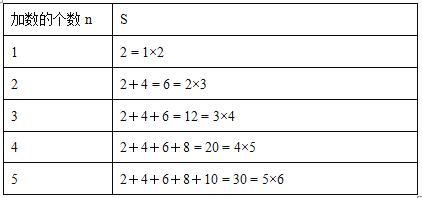
(1)当n=6时, S的值为__________.
(2)根据上题的规律计算:26+28+30+…+60的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,过一点分别作坐标轴的垂线,若垂线与坐标轴围成矩形的周长与面积相等,则这个点叫做“和谐点”.
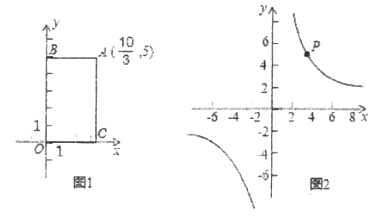
如图1,矩形ABOC的周长与面积相等,则点A是“和谐点”,
(1)点![]() ,其中“和谐点”是_______;
,其中“和谐点”是_______;
(2)如图2,若点![]() 是双曲线
是双曲线![]() 上的“和谐点”,请直接写出所有满足条件的P点坐标__________________________.
上的“和谐点”,请直接写出所有满足条件的P点坐标__________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在一次大课间活动中,采用了四钟活动形式:A、跑步,B、跳绳,C、做操,D、游戏.全校学生都选择了一种形式参与活动,小杰对同学们选用的活动形式进行了随机抽样调查,根据调查统计结果,绘制了不完整的统计图.
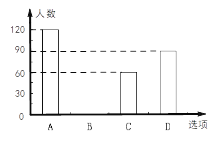
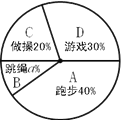
请结合统计图,回答下列问题:
(1)本次调查学生共 人, ![]() = ,并将条形图补充完整;
= ,并将条形图补充完整;
(2)如果该校有学生2000人,请你估计该校选择“跑步”这种活动的学生约有多少人?
(3)学校让每班在A、B、C、D四钟活动形式中,随机抽取两种开展活动,请用树状图或列表的方法,求每班抽取的两种形式恰好是“跑步”和“跳绳”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
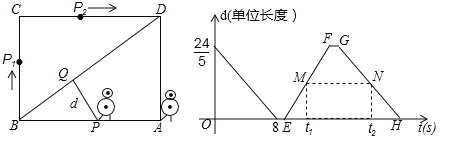
【题目】(2017江苏省苏州市)某校机器人兴趣小组在如图①所示的矩形场地上开展训练.机器人从点A出发,在矩形ABCD边上沿着A→B→C→D的方向匀速移动,到达点D时停止移动.已知机器人的速度为1个单位长度/s,移动至拐角处调整方向需要1s(即在B、C处拐弯时分别用时1s).设机器人所用时间为t(s)时,其所在位置用点P表示,P到对角线BD的距离(即垂线段 PQ的长)为d个单位长度,其中d与t的函数图象如图②所示.
(1)求AB、BC的长;
(2)如图②,点M、N分别在线段EF、GH上,线段MN平行于横轴,M、N的横坐标分别为t1、t2.设机器人用了t1(s)到达点P1处,用了t2(s)到达点P2处(见图①).若CP1+CP2=7,求t1、t2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com