
【题目】已知二次函数y=ax2+bx+c的图象经过点(2,-5),顶点坐标为(-1,4),直线l的解析式为y=2x+m.
(1)求抛物线的解析式;
(2)若抛物线与直线l有两个公共点,求![]() 的取值范围;
的取值范围;
(3)若直线l与抛物线只有一个公共点P,求点P的坐标;
(4)设抛物线与![]() 轴的交点分别为A、B,求在(3)的条件下△PAB的面积.
轴的交点分别为A、B,求在(3)的条件下△PAB的面积.
【答案】(1)y=-x2-2x+3;(2)当m<7时,抛物线与直线l有两个公共点;(3)点P的坐标为(-2,3);(4)SPAB=6.
【解析】
(1)由抛物线顶点坐标可得二次函数y=a(x+1)2+4,将点(2,-5)代入,即可得到抛物线的解析式,
(2)由抛物线的解析式及直线l的解析式联立,利用△即可求出抛物线与直线l有两个公共点m的取值范围,
(3)由抛物线的解析式及直线l的解析式联立,利用△=0时求出m的值,再联立即可求出点P的坐标,
(4)抛物线的解析式求出AB的长,利用S△PAB=![]() ABP纵坐标,即可求出△PAB的面积.
ABP纵坐标,即可求出△PAB的面积.
解:(1)∵抛物线顶点坐标为(-1,4),
∴它的解析式为y=a(x+1)2+4,将点(2,-5)代入,得a=-1.
∴抛物线的解析式为:y=-x2-2x+3.
(2)由![]() ,
,
得x2-4x+m-3=0,
∴△=16-4(m-3)=-4m+28.
当-4m+28>0时,解得m<7.
即当m<7时,抛物线与直线l有两个公共点.
(3)由(2)知:当抛物线与直线l只有一个公共点时,m=7,
由![]()
解得![]() ,
,
即点P的坐标为(-2,3).
(4)∵抛物线的解析式为:y=-x2-2x+3.抛物线与x轴的交点分别为A、B,
∴令0=-x2-2x+3,得x1=-3,x2=1,
∴AB=4,
∴S△PAB=![]() ABP纵坐标=
ABP纵坐标=![]() ×4×3=6.
×4×3=6.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).

A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
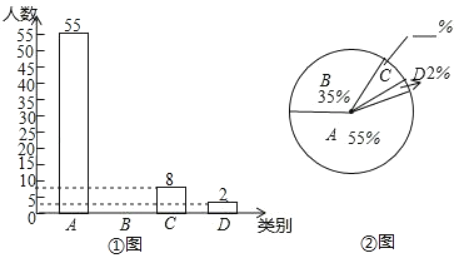
【题目】我省某地区为了了解2017年初中毕业生毕业去向,对部分九年级学生进行了抽样调查,就九年级学生毕业后的四种去向:A.读重点高中;B.读职业高中;C.直接进入社会就业;D.其他(如出国等)进行数据统计,并绘制了两幅不完整的统计图(如①图,如②图)
(1)该地区共调查了_____名九年级学生;
(2)将两幅统计图中不完整的部分补充完整;
(3)若该地区2017年初中毕业生共有4000人,请估计该地区今年初中毕业生中读重点高中的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a﹣2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )

A.①② B.①④ C.①③④ D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
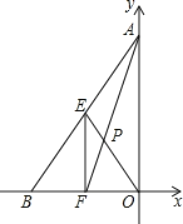
【题目】如图,在平面直角坐标系中,O为坐标原点,点A,B的坐标分别为(0,4),(﹣3,0),E为AB的中点,EF∥AO交OB于点F,AF与EO交于点P,则EP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
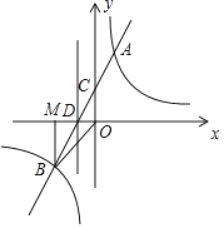
【题目】如图,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A,B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为点M,BM=OM=2,点A的纵坐标为4.
(k≠0)的图象交于第一、三象限内的A,B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为点M,BM=OM=2,点A的纵坐标为4.
(1)求该反比例函数和一次函数的表达式;
(2)直线AB交x轴于点D,过点D作直线l⊥x轴,如果直线l上存在点P,坐标平面内存在点Q.使四边形OPAQ是矩形,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极配合我市文明城市创建,居委会组织了两个检查组,分别对辖区内新华园、清华园、德才园、御花园四个小区“垃圾分类”和“违规停车”的情况进行抽查,每个检查组随机抽取辖区内的一个小区进行检查.
(1)“违规停车”检查组抽到新华园小区的概率为_____;
(2)求两个组恰好同时抽到御花园小区进行检查的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行“校园朗读者”朗诵大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
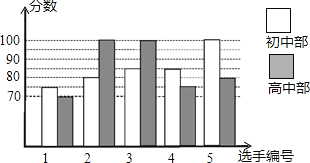
(1)根据图示填写表格;
平均分(分) | 中位数(分) | 众数(分) | |
初中部 |
| 85 |
|
高中部 | 85 |
| 100 |
(2)结合两队成绩的平均数和中位数, 队的决赛成绩较好;
(3)已知高中代表队决赛成绩的方差为160,计算初中代表队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.(方差公式:S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2]
)2]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com