

分析 (1)根据图2,利用直接求与间接法分别表示出正方形面积,即可确定出所求等式;
(2)根据(1)中结果,求出所求式子的值即可;
(3)根据已知等式,做出相应图形,如图所示;
(4)根据题意列出关系式,即可确定出长方形较长的边.
解答 解:(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)∵a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2=(a+b+c)2-2(ab+ac+bc)=121-76=45;
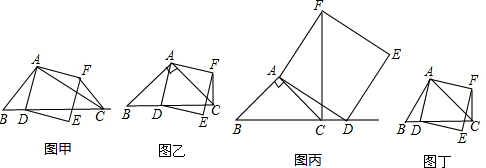
(3)如图所示:
(4)根据题意得:2a2+5ab+3b2=(2a+3b)(a+b),
则较长的一边为2a+3b.
故答案为:(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;(4)2a+3b
点评 此题考查了多项式乘以多项式,熟练掌握运算法则是解本题的关键.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:选择题
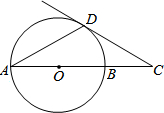 如图,AB是⊙O直径,C是AB延长线上一点,CD是⊙O的切线,D为切点,∠A=30°,AB=2cm,则CD的长为( )
如图,AB是⊙O直径,C是AB延长线上一点,CD是⊙O的切线,D为切点,∠A=30°,AB=2cm,则CD的长为( )| A. | 2cm | B. | $\frac{3}{2}$cm | C. | $\sqrt{3}$cm | D. | $\frac{\sqrt{3}}{2}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
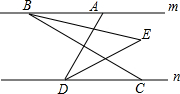 如图,已知直线m∥n,A、B是直线m上的任意两点,C、D是直线n上的任意两点,连AD、BC,∠ABC与∠ADC的平分线相交于点E,若∠BAD=80°.
如图,已知直线m∥n,A、B是直线m上的任意两点,C、D是直线n上的任意两点,连AD、BC,∠ABC与∠ADC的平分线相交于点E,若∠BAD=80°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
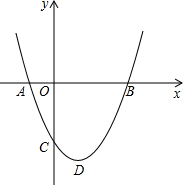 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中:
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中:| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,点A(0,4),B(3,0),以AB为边在第一象限内作正方形ABCD,直线l:y=kx+3.
在平面直角坐标系xOy中,点A(0,4),B(3,0),以AB为边在第一象限内作正方形ABCD,直线l:y=kx+3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com