
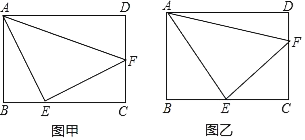
【题目】在矩形ABCD中,AB=3,BC=4,点E、F分别在BC与CD上,且∠EAF=45°.如图甲,若EA=EF,则EF=_____;如图乙,若CE=CF,则EF=_____.
【答案】![]()
![]() .
.
【解析】
(1)已知EA=EF,∠EAF=45°,由三角形的内角和得∠AEF=90°,∠AEB+∠FEC=90°,又因∠BAE+∠AEB=90°,等量代换得∠BAE=∠CEF,从而证明△ABE≌△ECF;EF的长可由勾股定理求出.
(2)作辅助线FM 和EN,已知△CEF,构建两个等腰△DEM,△BEN可求出线段DF,AM,FC,BE和AN的长;证明△ANE∽△FMA,再由两个三角形相似的性质求出相似比,解出x的值,由勾股定理(或三角函数)求出EF的长.
解:(1)如图甲所示:

∵EA=EF,
∴△AEF是等腰直角三角形,∠EAF=∠EFA,
∵∠EAF=45°,
∴∠EFA=45°,
又∵在△AEF中,∠EAF+∠EFA+∠AEF=180°,
∴∠AEF=180°﹣45°﹣45°=90°,
又∵∠AEB+∠AEF+∠FEC=180°,
∴∠AEB+∠FEC=90°,
又∵△ABE中,∠B+∠BAE+∠AEB=180°,
∠B=90°,
∴∠BAE+∠AEB=90°,
∴∠BAE=∠CEF,
在△ABE和△ECF中
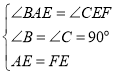 ,
,
∴△ABE≌△ECF(AAS)
∴AB=EC,BE=CF,
又∵AB=3,BC=4,
∴EC=3,CF=1,
在Rt△CEF中,由勾股定理得:
![]()
故答案为![]() .
.
(2)如图乙所示:
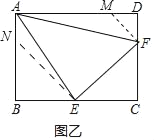
作DM=DF,BN=BE,分别交AD,AB于点M和点N,设MD=x,
∵四边形ABCD是矩形,
∴∠B=∠D=90°,
∴∠BNE=45°,∠DMF=90°,
又∵∠BNE+∠ENA=180°,∠FMD+∠FMA=180°,
∴∠ENA=135°,∠FMA=135°,
又∵∠EAF=45°,∠BAD=∠BAE+∠EAF+∠FAD=90°,
∴∠BAE+∠FAD=45°,
∵∠BAE+∠NEA=45°,
在△ANE和△FMA中
![]() ,
,
∴△ANE∽△FMA
∴![]() ;
;
又∵MD=x,∴DF=x,
∵CE=CF,AB=3,BC=4,
∴FC=EC=3﹣x,BE=BC-CE=4-(3-x)=x+1,AN=2﹣x,
∴ ,
,
解得:x=2![]() ﹣4或x=﹣2
﹣4或x=﹣2![]() ﹣4(舍去),
﹣4(舍去),
∴FC=3﹣(2![]() ﹣4)=7﹣2
﹣4)=7﹣2![]() ,
,
∴EF=![]() FC=
FC=![]() (7﹣2
(7﹣2![]() )=7
)=7![]() ﹣4
﹣4![]() .
.
故答案为7![]() ﹣4
﹣4![]() .
.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】为了给游客提供更好的服务,某景区随机对部分游客进行了关于“景区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.
满意度 | 人数 | 所占百分比 |
非常满意 | 12 | 10% |
满意 | 54 | m |
比较满意 | n | 40% |
不满意 | 6 | 5% |

根据图表信息,解答下列问题:
(1)本次调查的总人数为______,表中m的值为_______;
(2)请补全条形统计图;
(3)据统计,该景区平均每天接待游客约3600人,若将“非常满意”和“满意”作为游客对景区服务工作的肯定,请你估计该景区服务工作平均每天得到多少名游客的肯定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科研所计划建一幢宿舍楼,因为科研所实验中会产生辐射,所以需要有两项配套工程.①在科研所到宿舍楼之间修一条高科技的道路;②对宿含楼进行防辐射处理;已知防辐射费y万元与科研所到宿舍楼的距离xkm之间的关系式为y=ax+b(0≤x≤3).当科研所到宿舍楼的距离为1km时,防辐射费用为720万元;当科研所到宿含楼的距离为3km或大于3km时,辐射影响忽略不计,不进行防辐射处理,设修路的费用与x2成正比,且比例系数为m万元,配套工程费w=防辐射费+修路费.
(1)当科研所到宿舍楼的距离x=3km时,防辐射费y=____万元,a=____,b=____;
(2)若m=90时,求当科研所到宿舍楼的距离为多少km时,配套工程费最少?
(3)如果最低配套工程费不超过675万元,且科研所到宿含楼的距离小于等于3km,求m的范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
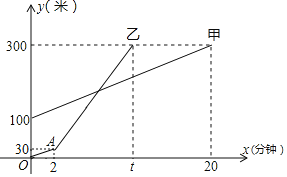
【题目】甲、乙两人相约周末沿同一条路线登山,甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题
(1)甲登山的速度是每分钟 米;乙在A地提速时,甲距地面的高度为 米;
(2)若乙提速后,乙的速度是甲登山速度的3倍;
①求乙登山全过程中,登山时距地面的高度y(米)与登山时间x(分钟)之间的函数解析式;
②乙计划在他提速后5分钟内追上甲,请判断乙的计划能实现吗?并说明理由;
(3)当x为多少时,甲、乙两人距地面的高度差为80米?
查看答案和解析>>
科目:初中数学 来源: 题型:
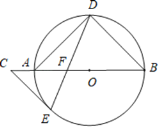
【题目】如图,AB是⊙O的直径,点D,E在⊙O上,∠B=2∠ADE,点C在BA的延长线上.
(Ⅰ)若∠C=∠DAB,求证:CE是⊙O的切线;
(Ⅱ)若OF=2,AF=3,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面内有一点P到△ABC的三个顶点的距离分别为PA、PB、PC,若有PA2=PB2+PC2则称点P为△ABC关于点A的勾股点.
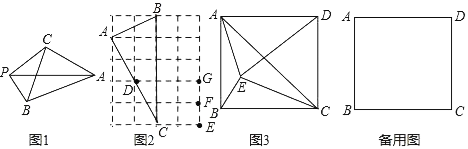
(1)如图2,在4×5的网格中,每个小正方形的长均为1,点A、B、C、D、E、F、G均在小正方形的顶点上,则点D是△ABC关于点 的勾股点;在点E、F、G三点中只有点 是△ABC关于点A的勾股点.
(2)如图3,E是矩形ABCD内一点,且点C是△ABE关于点A的勾股点,
①求证:CE=CD;②若DA=DE,∠AEC=120°,求∠ADE的度数.
(3)矩形ABCD中,AB=5,BC=6,E是矩形ABCD内一点,且点C是△ABE关于点A的勾股点,
①若△ADE是等腰三角形,求AE的长;②直接写出AE+![]() BE的最小值.
BE的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若用“*”表示一种运算规则,我们规定:a*b=ab﹣a+b,如:3*2=3×2﹣3+2=5.以下说法中错误的是( )
A. 不等式(﹣2)*(3﹣x)<2的解集是x<3
B. 函数y=(x+2)*x的图象与x轴有两个交点
C. 在实数范围内,无论a取何值,代数式a*(a+1)的值总为正数
D. 方程(x﹣2)*3=5的解是x=5
查看答案和解析>>
科目:初中数学 来源: 题型:
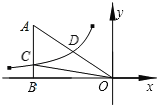
【题目】如图,已知双曲线![]() (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为_____.
(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
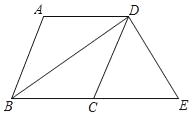
【题目】如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com