
����Ŀ���������ƻ���һ������¥����Ϊ������ʵ���л�������䣬������Ҫ�����������̣����ڿ�����������¥֮����һ���߿Ƽ��ĵ�·���ڶ���¥���з����䴦������֪�������y��Ԫ�������������¥�ľ���xkm֮��Ĺ�ϵʽΪy��ax+b(0��x��3)����������������¥�ľ���Ϊ1kmʱ�����������Ϊ720��Ԫ��������������¥�ľ���Ϊ3km�����3kmʱ������Ӱ����Բ��ƣ������з����䴦��������·�ķ�����x2�����ȣ��ұ���ϵ��Ϊm��Ԫ�������̷�w���������+��·�ѣ�
(1)��������������¥�ľ���x��3kmʱ���������y��____��Ԫ��a��____��b��____��
(2)��m��90ʱ��������������¥�ľ���Ϊ����kmʱ�������̷����٣�
(3)�����������̷Ѳ�����675��Ԫ���ҿ���������¥�ľ���С�ڵ���3km����m�ķ�Χ��
���𰸡�(1)0����360��1080��(2)������Ϊ2����ʱ�������̷������٣�(3)0��m��80��
��������
(1)��x��1ʱ��y��720����x��3ʱ��y��0����x��y����y��ax+b��������⣻
(2)������Ŀ�������̷�w���������+��·�ѷ�0��x��3��x��3ʱ����.
����0��x��3ʱ�������̷�W��90x2��360x+1080������x��3ʱ��W��90x2���ֱ�����Сֵ���ɣ�
(3)0��x��3��W��mx2��360x+1080��(m��0)����Գ���x��![]() ��Ȼ�����ۣ�x��
��Ȼ�����ۣ�x��![]() =3ʱ��x��
=3ʱ��x��![]() ��3ʱ�������mȡֵ������⣮
��3ʱ�������mȡֵ������⣮
�⣺(1)��x��1ʱ��y��720����x��3ʱ��y��0����x��y����y��ax+b��
��ã�a����360��b��1080��
�ʴ�Ϊ��0����360��1080��
(2)����0��x��3ʱ�������̷�W��90x2��360x+1080��
����x��2ʱ��Wmin��720��
����x��3ʱ��W��90x2��
W��x�������
��x��3ʱ��Wmin��810��720��
��������Ϊ2����ʱ�������̷������٣�
(3)��0��x��3��
W��mx2��360x+1080��(m��0)����Գ���x��![]() ��
��
��x��![]() ��3ʱ������m��60��
��3ʱ������m��60��
Wmin��m(![]() )2��360(
)2��360(![]() )+1080��
)+1080��
��Wmin��675����ã�60��m��80��
��x��![]() ��3ʱ����m��60��
��3ʱ����m��60��
��x��3ʱ��Wmin��9m��675��
��ã�0��m��60��
�ʣ�0��m��80��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����������������˾ӳ��У���������һ���㳡����ֲ�ס������ֻ��ܣ����г����飬���ֻ��ܵ���ֲ����y��Ԫ������ֲ���x��m2��֮��ĺ�����ϵ��ͼ��ʾ�����ֻ��ܵ���ֲ����Ϊÿƽ����100Ԫ��
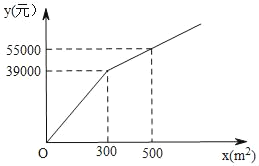
��1�������y��x�ĺ�����ϵʽ��
��2���㳡�ϼס������ֻ��ܵ���ֲ�����1200m2�������ֻ��ܵ���ֲ���������200m2���Ҳ��������ֻ��ܵ���ֲ�����2����
��������ֲ�ܷ���WԪ����ֲ���x��m2��֮��ĺ�����ϵʽ��
��Ӧ����������ס������ֻ��ܵ���ֲ�������ʹ��ֲ�ܷ���W���٣������ܷ���Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���D�DZ�BC�ϵĵ㣨��B��C���㲻�غϣ�������D��DE��AC��DF��AB���ֱ�AB��AC��E��F���㣬����˵����ȷ���ǣ�������

A. ��AD��BC�����ı���AEDF�Ǿ���
B. ��AD��ֱƽ��BC�����ı���AEDF�Ǿ���
C. ��BD=CD�����ı���AEDF������
D. ��ADƽ�֡�BAC�����ı���AEDF������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
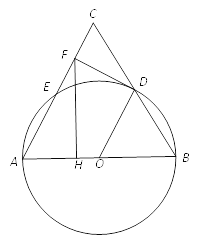
����Ŀ����ͼ������ABC�У��Ե�ABΪֱ���ġ�O�ֱ���AC��BC���ڵ�E��D����BD=CD��
��1����֤����B����C ��
��2������D��DF��OD������F��FH��AB����AB=5��CD=![]() ����AH��ֵ��
����AH��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʦ����Ⱥ��������һ��ͼ�����߶�ABΪ�����������ABCDE����������ABG������AC��DG������ΪF��������λͬѧ��˵������ȷ����( )
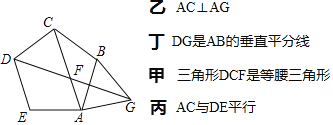
A. ��B. ��C. ��D. ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
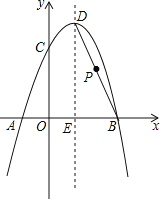
����Ŀ����ͼ��������y����x2+bx+c����A����1��0����B��3��0�����㣬����y�ύ�ڵ�C����D�������ߵĶ��㣬�����߶Գ���DE��x���ڵ�E������BD��
��1����A��B��C����������ߵĺ�������ʽ��
��2����P���߶�BD��һ�㣬��PE��PCʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ���������������ϴ������е�A��B�����߶�AB�����������ƶ����ƶ�����߶μ�ΪA��B�䣬��Ҫ��������и�С��
��1������AΪ����ԭ�㣬��B��ʾ������4������A��ǡ����AB���е�ʱ�������ϵ�B���ʾ����Ϊ�� ��
��2�����A��ʾ����Ϊm����A���ʾ����Ϊn����ԭ�����߶�A��B֮��ʱ������|m|+|n|+|m��n|��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�AB��3��BC��4����E��F�ֱ���BC��CD�ϣ��ҡ�EAF��45��.��ͼ�ף���EA��EF����EF��_____����ͼ�ң���CE��CF����EF��_____��
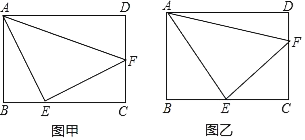
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
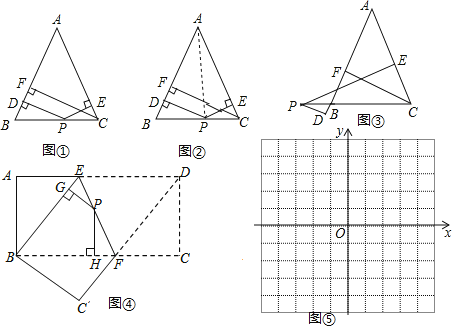
����Ŀ���������龳���ڡ�ABC�У�AB��AC����PΪBC����ֱ���ϵ���һ�㣬����P��PD��AB��PE��AC������ֱ�ΪD��E������C��CF��AB������ΪF����P��BC����ʱ����ͼ1������֤��PD+PE��CF��
֤��˼·�ǣ���ͼ2������AP���ɡ�ABP���ACP���֮�͵��ڡ�ABC���������֤�ã�PD+PE��CF������Ҫ֤����
����ʽ̽������1������P��CB�ӳ�����ʱ�������������䣨��ͼ3������̽��PD��PE��CF֮���������ϵ��˵�����ɣ�
��������������������۵ľ���ͷ�������������⣺
���������ã���2����ͼ4����������ABCD��EF�۵���ʹ��D���ڵ�B�ϣ���C���ڵ�C�䴦����PΪ�ۺ�EF�ϵ���һ�㣬����P��PG��BE��PH��BC������ֱ�ΪG��H����AD��16��CF��6����PG+PH��ֵ��
��Ǩ����չ����3����ֱ������ϵ�У�ֱ��l1��y��-![]() x+8��ֱ��l2��y����2x+8�ཻ�ڵ�A��ֱ��l1��l2��x��ֱ��ڵ�B����C����P��ֱ��l2��һ�����㣬����P��ֱ��l1�ľ���Ϊ2�����P�����꣮
x+8��ֱ��l2��y����2x+8�ཻ�ڵ�A��ֱ��l1��l2��x��ֱ��ڵ�B����C����P��ֱ��l2��һ�����㣬����P��ֱ��l1�ľ���Ϊ2�����P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com