
【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线对称轴DE交x轴于点E,连接BD.
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标.
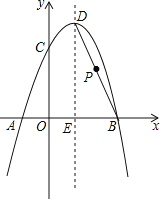
【答案】(1)y=﹣x2+2x+3;(2)点P的坐标为(2,2).
【解析】
(1)利用待定系数法求出过A,B,C三点的抛物线的函数表达式;
(2)连接PC、PE,利用公式求出顶点D的坐标,利用待定系数法求出直线BD的解析式,设出点P的坐标为(x,﹣2x+6),利用勾股定理表示出PC2和PE2,根据题意列出方程,解方程求出x的值,计算求出点P的坐标.
解:(1)∵抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,
∴![]() ,解得
,解得![]() ,
,
∴所求的抛物线的函数表达式为y=﹣x2+2x+3;
(2)如图,连接PC,PE.
抛物线的对称轴为x=![]() =1.
=1.
当x=1时,y=4,
∴点D的坐标为(1,4).
设直线BD的解析式为y=kx+b,
则![]() ,
,
解得![]() .
.
∴直线BD的解析式为:y=2x+6,
设点P的坐标为(x,﹣2x+6),又C(0,3),E(1,0),
则PC2=x2+(3+2x﹣6)2,PE2=(x﹣1)2+(﹣2x+6)2,
∵PC=PE,
∴x2+(3+2x﹣6)2=(x﹣1)2+(﹣2x+6)2,
解得,x=2,
则y=﹣2×2+6=2,
∴点P的坐标为(2,2).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问卷调查,调查结果为“A非常了解”、“B了解”、“C基本了解”三个等级,并根据调查结果制作了如下两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
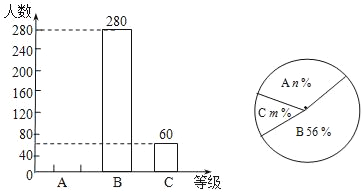
(1)本次调查的人数为 ;
(2)补全条形统计图;
(3)若该市约有市民100万人,请你根据抽样调查的结果,估计该市大约有多少人对“社会主义核心价值观”达到“A非常了解”的程度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(m,2),B(﹣3,n)两点关于原点O对称,反比例函数y=![]() 的图象经过点A.
的图象经过点A.
(1)求反比例函数的解析式并判断点B是否在这个反比例函数的图象上;
(2)点P(x1,y1)也在这个反比例函数的图象上,﹣3<x1<m且x1≠0,请直接写出y1的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O与直线l1相离,圆心O到直线l1的距离OB=2![]() ,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC=( )
,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC=( )
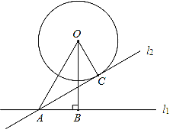
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科研所计划建一幢宿舍楼,因为科研所实验中会产生辐射,所以需要有两项配套工程.①在科研所到宿舍楼之间修一条高科技的道路;②对宿含楼进行防辐射处理;已知防辐射费y万元与科研所到宿舍楼的距离xkm之间的关系式为y=ax+b(0≤x≤3).当科研所到宿舍楼的距离为1km时,防辐射费用为720万元;当科研所到宿含楼的距离为3km或大于3km时,辐射影响忽略不计,不进行防辐射处理,设修路的费用与x2成正比,且比例系数为m万元,配套工程费w=防辐射费+修路费.
(1)当科研所到宿舍楼的距离x=3km时,防辐射费y=____万元,a=____,b=____;
(2)若m=90时,求当科研所到宿舍楼的距离为多少km时,配套工程费最少?
(3)如果最低配套工程费不超过675万元,且科研所到宿含楼的距离小于等于3km,求m的范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与直线y=x交于(1,1)和(3,3)两点,现有以下结论:①b2﹣4c>0;②3b+c+6=0;③当x2+bx+c>![]() 时,x>2;④当1<x<3时,x2+(b﹣1)x+c<0,其中正确的序号是( )
时,x>2;④当1<x<3时,x2+(b﹣1)x+c<0,其中正确的序号是( )
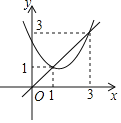
A. ①②④B. ②③④C. ②④D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
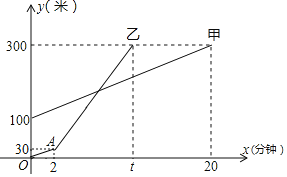
【题目】甲、乙两人相约周末沿同一条路线登山,甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题
(1)甲登山的速度是每分钟 米;乙在A地提速时,甲距地面的高度为 米;
(2)若乙提速后,乙的速度是甲登山速度的3倍;
①求乙登山全过程中,登山时距地面的高度y(米)与登山时间x(分钟)之间的函数解析式;
②乙计划在他提速后5分钟内追上甲,请判断乙的计划能实现吗?并说明理由;
(3)当x为多少时,甲、乙两人距地面的高度差为80米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面内有一点P到△ABC的三个顶点的距离分别为PA、PB、PC,若有PA2=PB2+PC2则称点P为△ABC关于点A的勾股点.
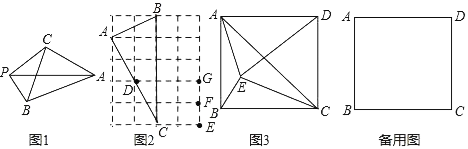
(1)如图2,在4×5的网格中,每个小正方形的长均为1,点A、B、C、D、E、F、G均在小正方形的顶点上,则点D是△ABC关于点 的勾股点;在点E、F、G三点中只有点 是△ABC关于点A的勾股点.
(2)如图3,E是矩形ABCD内一点,且点C是△ABE关于点A的勾股点,
①求证:CE=CD;②若DA=DE,∠AEC=120°,求∠ADE的度数.
(3)矩形ABCD中,AB=5,BC=6,E是矩形ABCD内一点,且点C是△ABE关于点A的勾股点,
①若△ADE是等腰三角形,求AE的长;②直接写出AE+![]() BE的最小值.
BE的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com