
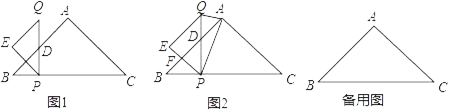
����Ŀ����ͼ1��ƽ������һ��P����ABC����������ľ���ֱ�ΪPA��PB��PC������PA2��PB2+PC2��Ƶ�PΪ��ABC���ڵ�A�Ĺ��ɵ㣮
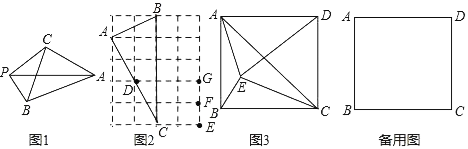
��1����ͼ2����4��5�������У�ÿ��С�����εij���Ϊ1����A��B��C��D��E��F��G����С�����εĶ����ϣ����D�ǡ�ABC���ڵ��� ���Ĺ��ɵ㣻�ڵ�E��F��G������ֻ�е��� ���ǡ�ABC���ڵ�A�Ĺ��ɵ㣮
��2����ͼ3��E�Ǿ���ABCD��һ�㣬�ҵ�C�ǡ�ABE���ڵ�A�Ĺ��ɵ㣬
����֤��CE��CD������DA��DE����AEC��120�㣬���ADE�Ķ�����
��3������ABCD�У�AB��5��BC��6��E�Ǿ���ABCD��һ�㣬�ҵ�C�ǡ�ABE���ڵ�A�Ĺ��ɵ㣬
������ADE�ǵ��������Σ���AE�ij�����ֱ��д��AE+![]() BE����Сֵ��
BE����Сֵ��
���𰸡���1��B��F����2���ټ��������ڡ�ADE��40�㣻��3����AE�ij�Ϊ![]() ��
��![]() ����AE+
����AE+![]() BE
BE![]() .
.
��������
��1����AD2��5��DC2��5��DB2��10����AD2+DC2��DB2������D����ABC���ڵ�B�Ĺ��ɵ㣻���FA2��FB2��FC2���õ�FA2+FB2��FC2������F����ABC���ڵ�A�Ĺ��ɵ㣮
��2�����ɾ������ʵá�ADC��90�����ɵ�AD2+DC2��AC2�����ݹ�������BC2+EC2��AC2������ΪAD��BC������CE��CD��
�����CED���������ݡ�AEC��120����CE��CD����ADC��90������������ʾ��ADE�������ڽǣ������������ڽǺ�180��Ϊ������ϵ�з��̣�����������������ADE��
��3������������C����ABE���ڵ�A�Ĺ��ɵ����Կɵ�CE��CD��5����Ϊ����ʹ�ã��١�ADE�ǵ������������3��������ۣ���ÿ�������ͼ�ٸ��ݾ������ʺ��ɶ������㣬������AE�ij������ɻ�ͼ��֪����BE��ACʱ��AE+![]() BEȡ����Сֵ������E�ֱ���AB��BC�Ĵ��ߣ�ͨ�����ɶ������㼴������𰸣�
BEȡ����Сֵ������E�ֱ���AB��BC�Ĵ��ߣ�ͨ�����ɶ������㼴������𰸣�
�⣺��1����DA2��12+22��5��DB2��12+32��10��DC2��DA2��5
��DB2��DC2+DA2
���D����ABC���ڵ�B�Ĺ��ɵ�
��EA2��42+42��32��EB2��22+52��29��EC2��4
���E������ABC�Ĺ��ɵ�
��FA2��32+42��25��FB2��22+42��20��FC2��12+22��5
��FA2��FB2+FC2
���F����ABC���ڵ�A�Ĺ��ɵ�
��GA2��42+22��20��GB2��22+32��13��GC2��22+22��8
���G������ABC�Ĺ��ɵ�
�ʴ�Ϊ��B��F��
��2����֤�����ߵ�C����ABE���ڵ�A�Ĺ��ɵ�
��CA2��CB2+CE2
���ı���ABCD�Ǿ���
��AB��CD��AD��BC����ADC��90��
��CA2��AD2+CD2��CB2+CD2
��CB2+CE2��CB2+CD2
��CE��CD
�����CED���������CDE����CED����
���ADE����ADC����CDE��90������
�ߡ�AEC��120��
���AED����AEC����CED��120������
��DA��DE
���DAE����DEA��120������
�ߡ�DAE+��DEA+��ADE��180��
��2��120��������+��90����������180��
������50��
���ADE��90����50����40��
��3���١߾���ABCD�У�AB��5��BC��6
��AD��BC��6��CD��AB��5
�ߵ�C����ABE���ڵ�A�Ĺ��ɵ�
��CE��CD��5
i����ͼ1��
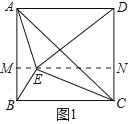
��DE��DA����DE��6
����E��MN��AB�ڵ�M����DC�ڵ�N
���AME����MND��90��
���ı���AMND�Ǿ���
��MN��AD��6��AM��DN
��AM��DN��x����CN��CD��DN��5��x
��Rt��DEN��EN2+DN2��DE2��Rt��CEN��EN2+CN2��CE2
��DE2��DN2��CE2��CN2
��62��x2��52����5��x��2
��ã�x��![]()
��EN�� ��AM��DN��
��AM��DN��![]()
��ME��MN��EN��6��![]()
��Rt��AME��AE��
ii����ͼ2��
��AE��DE����E��AD�Ĵ�ֱƽ������
����E��PQ��AD�ڵ�P����BC�ڵ�Q
��AP��DP��
![]() AD��3����APQ����PQC��90��
AD��3����APQ����PQC��90��
���ı���CDPQ�Ǿ���
��PQ��CD��5��CQ��PD��3
��Rt��CQE��EQ��![]()
��PE��PQ��EQ��1
��Rt��APE��AE��![]()
iii����ͼ3��
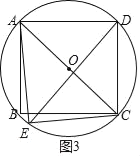
��AE��AD��6����AE2+CE2��AD2+CD2��AC2
���AEC��90��
ȡAC�е�O�����A��B��C��D����OΪԲ�ġ�OAΪ�뾶�ġ�O��
���EҲ�ڡ�O��
���E���ھ���ABCD�ڲ�������������
��������������ADE�ǵ��������Σ�AE�ij�Ϊ![]() ��
��![]() ��
��
�ڵ�BE��ACʱ��AE+![]() BEȡ����Сֵ��
BEȡ����Сֵ��
����E�ֱ���ER��AB�ڵ�R��ES��BC�ڵ�S,
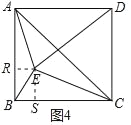
���ı���BRES�Ǿ��Σ���EBS���ACB����
���EBS����ACD
��tan��EBS��tan��ACD��![]()
��tan��EBS��![]()
��ES��6a��BS��5a����BE��![]() ��CS��6��5a��AR��5��6a
��CS��6��5a��AR��5��6a
��Rt��CES��CS2+ES2��CE2������6��5a��2+��6a��2��52
��ã�a1��![]() ����ȥ����a2��
����ȥ����a2��![]() ��61a2��60a����11
��61a2��60a����11
��Rt��ARE��AE��![]() ��
��![]()
��AE+![]() BE��
BE��![]() .
.


 �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д� ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ABC��90�㣬��ACB��30�㣬AC��6���ֽ�Rt��ABC�Ƶ�A˳ʱ����ת30��õ���AB��C�䣬��ͼ����Ӱ�������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
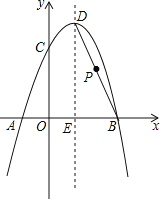
����Ŀ����ͼ��������y����x2+bx+c����A����1��0����B��3��0�����㣬����y�ύ�ڵ�C����D�������ߵĶ��㣬�����߶Գ���DE��x���ڵ�E������BD��
��1����A��B��C����������ߵĺ�������ʽ��
��2����P���߶�BD��һ�㣬��PE��PCʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��Ʒ�Ƶ������ʵ��ͼ��ʾ��ͼ����֪����BC��0.6�ף�����BC��֧��AC���ɵĽǡ�ACB��75�㣬֧��AF�ij�Ϊ2.5�ף����嶥��F�㵽����D�ľ���FD��1.4�ף�����ײ�֧��HE��֧��AF���ɵĽǡ�FHE��60�㣬������D������ľ��룮����ȷ��0.1�ף��ο����ݣ�cos75���0.3��sin75���0.9����tan75���3.7��![]() ��1.7��
��1.7��![]() ��1.4��
��1.4��
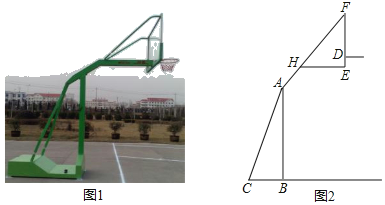
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�AB��3��BC��4����E��F�ֱ���BC��CD�ϣ��ҡ�EAF��45��.��ͼ�ף���EA��EF����EF��_____����ͼ�ң���CE��CF����EF��_____��
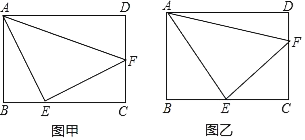
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���֪�ı���DOBC�Ǿ��Σ���D��0��4����B��6��0����������������y=![]() ��x��0����ͼ���߶�OC���е�A����DC�ڵ�E����BC�ڵ�F����ֱ��EF�Ľ���ʽΪy=k2x+b��
��x��0����ͼ���߶�OC���е�A����DC�ڵ�E����BC�ڵ�F����ֱ��EF�Ľ���ʽΪy=k2x+b��
��1������������ֱ��EF�Ľ���ʽ��
��2������OEF�������
��3������ͼ��ֱ��д������ʽk2x+b��![]() ��0�Ľ⼯��
��0�Ľ⼯��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�BDΪһ���Խ��ߣ�AD��BC��AD��2BC����ABD��90����EΪAD���е㣬����BE��
��1����֤���ı���BCDEΪ���Σ�
��2������AC����ACƽ�֡�BAD��BC��2����AC�ij���
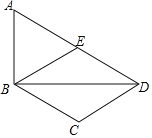
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ʵʩ��ҵ��ƶ������ƶ�����а��˻�ɽ��ֲijƷ������.�����ջڣ���֪�����ֵijɱ���Ϊ8Ԫ/ǧ�ˣ�Ͷ���г�����ʱ�������г����飬���ָ��������۲����������ÿ��������![]() (ǧ��)�����۵���
(ǧ��)�����۵���![]() (Ԫ/ǧ��)֮��ĺ�����ϵ��ͼ��ʾ.
(Ԫ/ǧ��)֮��ĺ�����ϵ��ͼ��ʾ.
(1)��![]() ��
��![]() �ĺ�����ϵʽ����д��
�ĺ�����ϵʽ����д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
(2)����Ʒ�����ֶ���Ϊ����ʱ��ÿ�����ۻ�õ����������������Ƕ��٣�
(3)ijũ�����깲��ժ����4800ǧ�ˣ���Ʒ�����ֵı�����Ϊ40�죬����(2)�л���������ķ�ʽ�������ۣ��ܷ��������������֣���˵������.
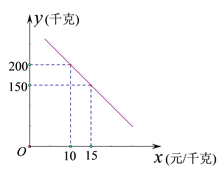
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���A��90�㣬AB��AC��4![]() ��һ����P�ӵ�B��������BC������ÿ��1����λ���ȵ��ٶ������˶��������C��ֹͣ���������˶������У�����P��PD��BC��Rt��ABC��ֱ�DZ��ཻ�ڵ�D���ӳ�PD����Q��ʹ��PD��QD����PQΪб����PQ���������ֱ��������PQE�����˶�ʱ��Ϊt�루t��0��
��һ����P�ӵ�B��������BC������ÿ��1����λ���ȵ��ٶ������˶��������C��ֹͣ���������˶������У�����P��PD��BC��Rt��ABC��ֱ�DZ��ཻ�ڵ�D���ӳ�PD����Q��ʹ��PD��QD����PQΪб����PQ���������ֱ��������PQE�����˶�ʱ��Ϊt�루t��0��
��1���������˶������У��ж�PE��AB��λ�ù�ϵ��
��2����ͼ2������D���߶�AB��ʱ������AQ��AP���Ƿ����������b��ʹ��AP��PQ�������ڣ������Ӧ��t��ֵ���������ڣ���˵�����ɣ�
��3����t��4ʱ����D������A����t��![]() ʱ����E�ڱ�AB�ϣ����ABC���PQE�ص����ֵ����ΪS��������������˶�������S��t֮��ĺ�����ϵʽ���Լ�д����Ӧ���Ա���t��ȡֵ��Χ���������4��t��
ʱ����E�ڱ�AB�ϣ����ABC���PQE�ص����ֵ����ΪS��������������˶�������S��t֮��ĺ�����ϵʽ���Լ�д����Ӧ���Ա���t��ȡֵ��Χ���������4��t��![]() ʱS�����ֵ��
ʱS�����ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com