
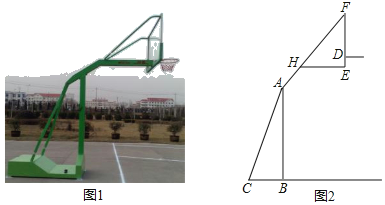
【题目】如图是某种品牌的篮球架实物图与示意图,已知底座BC=0.6米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.5米,篮板顶端F点到篮框D的距离FD=1.4米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离.(精确到0.1米.参考数据:cos75°≈0.3,sin75°≈0.9,.tan75°≈3.7,![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
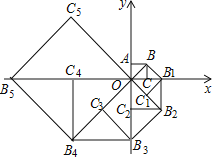
【题目】如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA,OC分别在x轴,y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2019的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O与直线l1相离,圆心O到直线l1的距离OB=2![]() ,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC=( )
,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC=( )
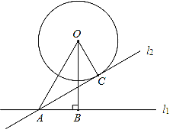
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与直线y=x交于(1,1)和(3,3)两点,现有以下结论:①b2﹣4c>0;②3b+c+6=0;③当x2+bx+c>![]() 时,x>2;④当1<x<3时,x2+(b﹣1)x+c<0,其中正确的序号是( )
时,x>2;④当1<x<3时,x2+(b﹣1)x+c<0,其中正确的序号是( )
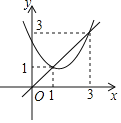
A. ①②④B. ②③④C. ②④D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
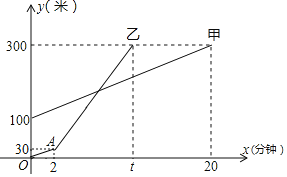
【题目】甲、乙两人相约周末沿同一条路线登山,甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题
(1)甲登山的速度是每分钟 米;乙在A地提速时,甲距地面的高度为 米;
(2)若乙提速后,乙的速度是甲登山速度的3倍;
①求乙登山全过程中,登山时距地面的高度y(米)与登山时间x(分钟)之间的函数解析式;
②乙计划在他提速后5分钟内追上甲,请判断乙的计划能实现吗?并说明理由;
(3)当x为多少时,甲、乙两人距地面的高度差为80米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角△ABC中,BC>AB>AC,求作一点P,使得∠BPC与∠A互补,甲、乙两人作法分别如下:
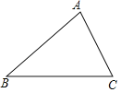
甲:以B为圆心,AB长为半径画弧交AC于P点,则P即为所求.
乙:作BC的垂直平分线和∠BAC的平分线,两线交于P点,则P即为所求.
对于甲、乙两人的作法,下列叙述正确的是( )
A. 两人皆正确B. 甲正确,乙错误C. 甲错误,乙正确D. 两人皆错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面内有一点P到△ABC的三个顶点的距离分别为PA、PB、PC,若有PA2=PB2+PC2则称点P为△ABC关于点A的勾股点.
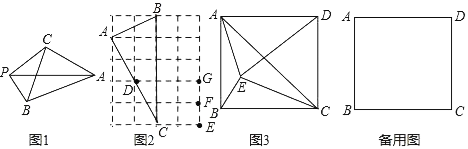
(1)如图2,在4×5的网格中,每个小正方形的长均为1,点A、B、C、D、E、F、G均在小正方形的顶点上,则点D是△ABC关于点 的勾股点;在点E、F、G三点中只有点 是△ABC关于点A的勾股点.
(2)如图3,E是矩形ABCD内一点,且点C是△ABE关于点A的勾股点,
①求证:CE=CD;②若DA=DE,∠AEC=120°,求∠ADE的度数.
(3)矩形ABCD中,AB=5,BC=6,E是矩形ABCD内一点,且点C是△ABE关于点A的勾股点,
①若△ADE是等腰三角形,求AE的长;②直接写出AE+![]() BE的最小值.
BE的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
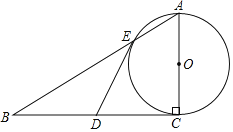
【题目】如图,已知Rt△ABC,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.
(1)求证:DE是⊙O的切线;
(2)若AE:EB=1:2,BC=12,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
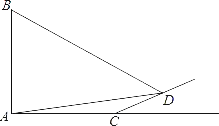
【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:![]() ,求旗杆AB的高度(
,求旗杆AB的高度(![]() ,结果精确到个位).
,结果精确到个位).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com