
【题目】如图,锐角△ABC中,BC>AB>AC,求作一点P,使得∠BPC与∠A互补,甲、乙两人作法分别如下:
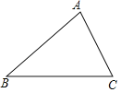
甲:以B为圆心,AB长为半径画弧交AC于P点,则P即为所求.
乙:作BC的垂直平分线和∠BAC的平分线,两线交于P点,则P即为所求.
对于甲、乙两人的作法,下列叙述正确的是( )
A. 两人皆正确B. 甲正确,乙错误C. 甲错误,乙正确D. 两人皆错误
【答案】A
【解析】
甲:根据作图可得AB=BP,利用等边对等角得:∠BAP=∠APB,由平角的定义可知:∠BPC+∠APB=180°,根据等量代换可作判断;
乙:利用角平分线的性质,作辅助线,证明Rt△BPG≌Rt△CPH(HL),可得∠BAC+∠BPC=180°,作判断即可.
解:甲:如图1,∵AB=BP,
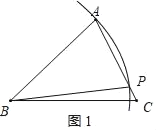
∴∠BAP=∠APB,
∵∠BPC+∠APB=180°
∴∠BPC+∠BAP=180°,
∴甲正确;
乙:如图2,过P作PG⊥AB于G,作PH⊥AC于H,
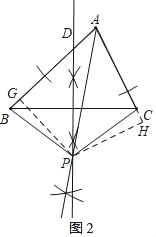
∵AP平分∠BAC,
∴PG=PH,
∵PD是BC的垂直平分线,
∴PB=PC,
∴Rt△BPG≌Rt△CPH(HL),
∴∠BPG=∠CPH,
∴∠BPC=∠GPH,
∵∠AGP=∠AHP=90°,
∴∠BAC+∠GPH=180°,
∴∠BAC+∠BPC=180°,
∴乙正确;
故选:A.


科目:初中数学 来源: 题型:
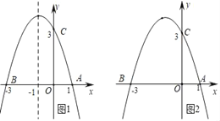
【题目】如图1,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)在(1)中抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(4)如图2,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
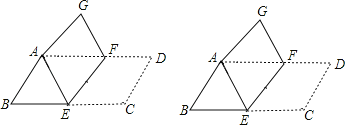
【题目】如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处.
(1)连接CF,求证:四边形AECF是菱形;
(2)若E为BC中点,BC=26,tan∠B=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为 .
问题探究
(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
问题解决
(3)如图③所示,AB、AC、BC是某新区的三条规划路其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F.也就是,分别在![]() 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).
、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).



图① 图② 图③
查看答案和解析>>
科目:初中数学 来源: 题型:
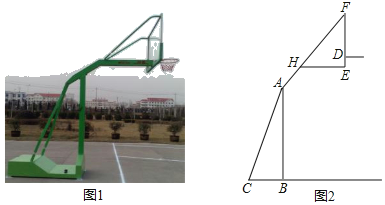
【题目】如图是某种品牌的篮球架实物图与示意图,已知底座BC=0.6米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.5米,篮板顶端F点到篮框D的距离FD=1.4米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离.(精确到0.1米.参考数据:cos75°≈0.3,sin75°≈0.9,.tan75°≈3.7,![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速的普及,根据国家信息中心发布的中国分享经济发展报告2017显示,参与共享经济活动超6 亿人,比上一年增加约1亿人.
(1)为获得北京市市民参与共享经济活动信息,下列调查方式中比较合理的是 ;
A.对某学校的全体同学进行问卷调查
B.对某小区的住户进行问卷调查
C.在全市里的不同区县,选取部分市民进行问卷调查
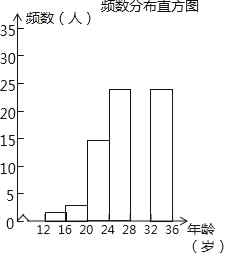
(2)调查小组随机调查了延庆区市民骑共享单车情况,某社区年龄在12~36岁的人有1000人,从中随机抽取了100人,统计了他们骑共享单车的人数,并绘制了如下不完整的统计图表.如图所示.骑共享单车的人数统计表
年龄段(岁) | 频数 | 频率 |
12≤x<16 | 2 | 0.02 |
16≤x<20 | 3 | 0.03 |
20≤x<24 | 15 | a |
24≤x<28 | 25 | 0.25 |
28≤x<32 | b | 0.30 |
32≤x<36 | 25 | 0.25 |
根据以上信息解答下列问题:
①统计表中的a= ;b= ;
②补全频数分布直方图;
③试估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=![]() (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b﹣![]() >0的解集.
>0的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从下列4个函数:①y=3x﹣2;②y=![]() (x<0);③y=
(x<0);③y=![]() (x>0);④y=﹣x2(x<0)中任取一个,函数值y随自变量x的增大而增大的概率是( )
(x>0);④y=﹣x2(x<0)中任取一个,函数值y随自变量x的增大而增大的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com