
【题目】从下列4个函数:①y=3x﹣2;②y=![]() (x<0);③y=
(x<0);③y=![]() (x>0);④y=﹣x2(x<0)中任取一个,函数值y随自变量x的增大而增大的概率是( )
(x>0);④y=﹣x2(x<0)中任取一个,函数值y随自变量x的增大而增大的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
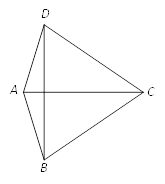
【题目】如图,在四边形ABCD中,AB=AD,AC是∠BAD的角平分线.
(1)求证:△ABC≌△ADC.
(2)若∠BCD=60°,AC=BC,求∠ADB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
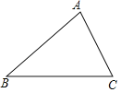
【题目】如图,锐角△ABC中,BC>AB>AC,求作一点P,使得∠BPC与∠A互补,甲、乙两人作法分别如下:
甲:以B为圆心,AB长为半径画弧交AC于P点,则P即为所求.
乙:作BC的垂直平分线和∠BAC的平分线,两线交于P点,则P即为所求.
对于甲、乙两人的作法,下列叙述正确的是( )
A. 两人皆正确B. 甲正确,乙错误C. 甲错误,乙正确D. 两人皆错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=2AC,点A(2,0)、B(0,4),点C在第一象限内,双曲线y=![]() (x>0)经过点C.将△ABC沿y轴向上平移m个单位长度,使点A恰好落在双曲线上,则m的值为________.
(x>0)经过点C.将△ABC沿y轴向上平移m个单位长度,使点A恰好落在双曲线上,则m的值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
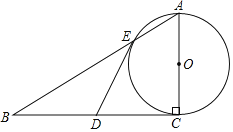
【题目】如图,已知Rt△ABC,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.
(1)求证:DE是⊙O的切线;
(2)若AE:EB=1:2,BC=12,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
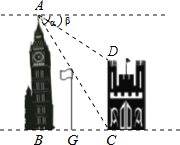
【题目】如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底部G点为BC的中点,求矮建筑物的高CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日常生活中我们经常会使用到订书机,如图MN是装订机的底座,AB是装订机的托板,始终与底座平行,连接杆DE的D点固定,点E从A向B处滑动,压柄BC可绕着转轴B旋转.已知压柄BC的长度为15cm,BD=5cm,压柄与托板的长度相等.
(1)当托板与压柄夹角∠ABC=37°时,如图①点E从A点滑动了2cm,求连接杆DE的长度;
(2)当压柄BC从(1)中的位置旋转到与底座AB的夹角∠ABC=127°,如图②.求这个过程中点E滑动的距离.(答案保留根号)(参考数据:sin37°≈0.6,cos37°≈0.8.tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,m),B(﹣2,﹣3)是直线AB和某反比例函数的图象的两个交点.
(1)求直线AB和反比例函数的解析式;
(2)观察图象,直接写出当x满足什么范围时,直线AB在双曲线的下方;
(3)反比例函数的图象上是否存在点C,使得△OBC的面积等于△OAB的面积?如果不存在,说明理由;如果存在,求出满足条件的所有点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次大规模的统计中发现英文文献中字母![]() 使用的频率在
使用的频率在![]() 附近,而字母
附近,而字母![]() 使用的频率大约为
使用的频率大约为![]() ,如果这次统计是可信的,那么下列说法正确吗?试说明理由 .
,如果这次统计是可信的,那么下列说法正确吗?试说明理由 .
(1)在英文文献中字母![]() 出现的概率在
出现的概率在![]() 左右,字母
左右,字母![]() 出现的概率在
出现的概率在![]() 左右;
左右;
(2)如果再去统计一篇约含![]() 个字母的英文文献,那么字母
个字母的英文文献,那么字母![]() 出现的概率一定会非常接近
出现的概率一定会非常接近![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com