
����Ŀ�����ճ����������Ǿ�����ʹ�õ����������ͼMN��װ�����ĵ�����AB��װ�������а壬ʼ�������ƽ�У����Ӹ�DE��D��̶�����E��A��B��������ѹ��BC������ת��B��ת����֪ѹ��BC�ij���Ϊ15cm��BD��5cm��ѹ�����а�ij�����ȣ�
��1�����а���ѹ���нǡ�ABC��37��ʱ����ͼ����E��A�㻬����2cm�������Ӹ�DE�ij��ȣ�
��2����ѹ��BC�ӣ�1���е�λ����ת�������AB�ļнǡ�ABC��127�㣬��ͼ��������������е�E�����ľ��룮���𰸱������ţ����ο����ݣ�sin37���0.6��cos37���0.8��tan37���0.75��

���𰸡���1�����Ӹ�DE�ij���Ϊ3![]() cm��2����������е�E�����ľ���Ϊ��16��
cm��2����������е�E�����ľ���Ϊ��16��![]() ��cm
��cm
��������
��1����DH��BE��H����Rt��BDH�������Ǻ������DH��BH�������EH����������DEH���ù��ɶ����������DE����2����DH��AB���ӳ����ڵ�H����Rt��DBH��Rt��DEH�У������Ǻ����ֱ����BH��DH��EB�ij����Ӷ������ ��E�����ľ��룮
��1����ͼ�٣���DH��BE��H��
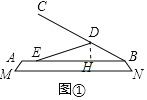
��Rt��BDH�У���DHB��90�㣬BD��5����ABC��37�㣬
��![]() = sin37�㣬
= sin37�㣬![]() ��cos37�㣬
��cos37�㣬
��DH��5sin37���5��0.6��3��cm����BH��5cos37�㣽5��0.8��4��cm����
��AB��BC��15cm��AE��2cm��
��EH��AB��AE��BH��15��2��4��9��cm����
��DE��![]()
�����Ӹ�DE�ij���Ϊ![]() cm��
cm��
��2����ͼ�ڣ���DH��AB���ӳ����ڵ�H��
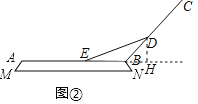
�ߡ�ABC��127�㣬
���DBH��53�㣬��BDH��37�㣬
��Rt��DBH�У�![]() ��sin37�㣽0.6��
��sin37�㣽0.6��
��BH��3cm��
��DH��4cm��
��Rt��DEH��EH2+DH2��DE2��
�ࣨEB+3��2+16��90��
��EB����![]() ����cm����
����cm����
���E�����ľ���Ϊ��15����![]() ����2����16��
����2����16��![]() ����cm����
����cm����
����������е�E�����ľ���Ϊ��16��![]() ��cm��
��cm��


 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
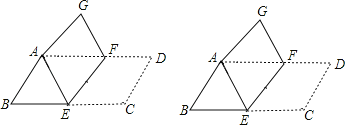
����Ŀ����ͼ����ƽ���ı���ABCDֽƬ��EF�۵���ʹ��C���A�غϣ���D���ڵ�G����
(1)����CF����֤���ı���AECF�����Σ�
(2)��EΪBC�е㣬BC��26��tan��B��![]() ����EF�ij���
����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���֪�ı���DOBC�Ǿ��Σ���D��0��4����B��6��0����������������y=![]() ��x��0����ͼ���߶�OC���е�A����DC�ڵ�E����BC�ڵ�F����ֱ��EF�Ľ���ʽΪy=k2x+b��
��x��0����ͼ���߶�OC���е�A����DC�ڵ�E����BC�ڵ�F����ֱ��EF�Ľ���ʽΪy=k2x+b��
��1������������ֱ��EF�Ľ���ʽ��
��2������OEF�������
��3������ͼ��ֱ��д������ʽk2x+b��![]() ��0�Ľ⼯��
��0�Ľ⼯��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������4����������y��3x��2����y=![]() ��x��0������y=
��x��0������y=![]() ��x��0������y����x2��x��0������ȡһ��������ֵy���Ա���x�����������ĸ����ǣ�������
��x��0������y����x2��x��0������ȡһ��������ֵy���Ա���x�����������ĸ����ǣ�������
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
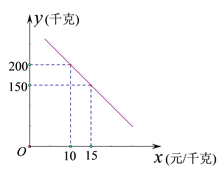
����Ŀ��ij����ʵʩ��ҵ��ƶ������ƶ�����а��˻�ɽ��ֲijƷ������.�����ջڣ���֪�����ֵijɱ���Ϊ8Ԫ/ǧ�ˣ�Ͷ���г�����ʱ�������г����飬���ָ��������۲����������ÿ��������![]() (ǧ��)�����۵���
(ǧ��)�����۵���![]() (Ԫ/ǧ��)֮��ĺ�����ϵ��ͼ��ʾ.
(Ԫ/ǧ��)֮��ĺ�����ϵ��ͼ��ʾ.
(1)��![]() ��
��![]() �ĺ�����ϵʽ����д��
�ĺ�����ϵʽ����д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
(2)����Ʒ�����ֶ���Ϊ����ʱ��ÿ�����ۻ�õ����������������Ƕ��٣�
(3)ijũ�����깲��ժ����4800ǧ�ˣ���Ʒ�����ֵı�����Ϊ40�죬����(2)�л���������ķ�ʽ�������ۣ��ܷ��������������֣���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
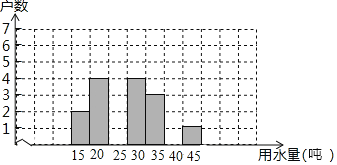
����Ŀ���±���2018�����·�ij����С�������ȡ20���������ˮ�������
����ˮ��/�� | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
���� | 2 | 4 | m | 4 | 3 | 0 | 1 |
��1�����m���� �������仭����20����ͥ���·��õ���������ͳ��ͼ��
��2�����ϱ����й���Ϣ��������ҳ��±��е�ͳ�������������������У�
ͳ�������� | ���� | ��λ�� | ƽ���� |
���� | �� �� | �� �� | �� �� |
��3��Ϊ�˳�������Լ��ˮ��ɫ����������ʶ������������ˮ��˾ʵ�С��ݼ���ˮ������Ʒѡ����۸�����£�
����ˮ�ݼ��� | ��30�����ڣ� | ������30�ֵIJ��֣� |
���ۣ�Ԫ/�֣� | 2.4 | 4 |
�����С����500����ͥ�������������ݣ�������С�����·��ж��ٻ���ͥ�ڢ���
��4�����ϱ��շѣ����ij�û����½�ˮ��120Ԫ�����ʸ��û�������ˮ���ٶ֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
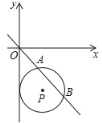
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���P��Բ���ǣ�2��a�����뾶Ϊ2��ֱ��y����x���P�ཻ��A��B���㣬����AB�ij�Ϊ2![]() ����a��ֵ�ǣ�������
����a��ֵ�ǣ�������
A. ��2![]() B. ��2+
B. ��2+![]() C. ��2��
C. ��2��![]() D. ��2��
D. ��2��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=3��BC=4������P��A���������A��B��C�ķ�����AB��BC���ƶ�����PA=x����D��ֱ��PA�ľ���Ϊy����y����x�ĺ���ͼ������ǣ� ��

A. B.
B.
C. D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
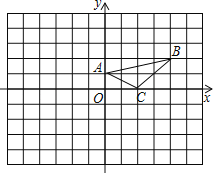
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A��0��1����B��4��2����C��2��0����
��1������ABC��y�ᷭ�۵õ���A1B1C1��������A1B1C1��
��2������ABC���ŵ㣨��1����1����ת180��õ���A2B2C2��������A2B2C2��
��3���߶�B2C2���Կ������߶�B1C1����ƽ��ֱ������ϵ��ijһ����ʱ����ת�õ���ֱ��д����ת���ĵ�����Ϊ�� ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com