
����Ŀ���ӹ������������������ȹ������е�������ɡ�ȹ�����Ʒ����ʽ�����Ĺ�������ģʽ�ڸ�������Ѹ�ٵ��ռ������ݹ�����Ϣ���ķ������й��������÷�չ����2017��ʾ�����빲�����û��6 ���ˣ�����һ������Լ1���ˣ�
��1��Ϊ��ñ�����������빲�����û��Ϣ�����е��鷽ʽ�бȽϺ��������� ����
A����ijѧУ��ȫ��ͬѧ�����ʾ�����
B����ijС����ס�������ʾ�����
C����ȫ����IJ�ͬ���أ�ѡȡ������������ʾ�����
��2������С����������������������ﹲ�����������ij����������12��36�������1000�ˣ����������ȡ��100�ˣ�ͳ���������ﹲ�������������������������²�������ͳ��ͼ������ͼ��ʾ���ﹲ������������ͳ�Ʊ�
����Σ��꣩ | Ƶ�� | Ƶ�� |
12��x��16 | 2 | 0.02 |
16��x��20 | 3 | 0.03 |
20��x��24 | 15 | a |
24��x��28 | 25 | 0.25 |
28��x��32 | b | 0.30 |
32��x��36 | 25 | 0.25 |
����������Ϣ����������⣺
��ͳ�Ʊ��е�a���� ����b���� ����
�ڲ�ȫƵ���ֲ�ֱ��ͼ��
���Թ����������������20�굽32�꣨��20�꣬����32�꣩�ﹲ�����������ж����ˣ�
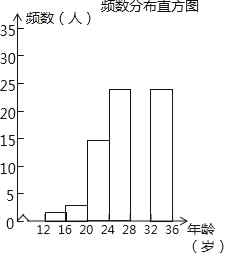
���𰸡���1��C����2����0.15��30���ڼ��������۹����������������20�굽32�꣨��20�꣬����32�꣩�ﹲ������������700�ˣ�
��������
��1�����ݳ�������Ķ���ɵã�
��2���ٸ�����Ƶ�ʣ�Ƶ�����������ɷֱ����a��b��ֵ��
���ɢ����������ݿɲ�ȫͼ�Σ�
�����������������е�3��4��5���Ƶ��֮�Ϳɵô𰸣�
�⣺��1�����鷽ʽ�бȽϺ�������C��
�ʴ�ΪC��
��2����a��15��100��0.15��b��100��0.3��30��
�ʴ�Ϊ0.15��30��
�ڲ�ȫͼ�����£�
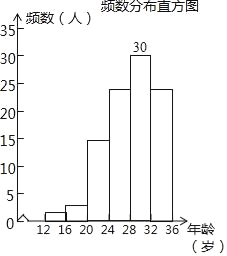
��1000����0.15+0.25+0.3����700���ˣ���
�𣺹����������������20�굽32�꣨��20�꣬����32�꣩�ﹲ������������700�ˣ�


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д� �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ����
����![]() ���ڵ�
���ڵ�![]() ����
����![]() ������һ��
������һ��![]() ������
������![]() .
.

��1������κ����ı���ʽ��
��2������![]() ��������
Ϊ��������![]() �Ḻ�����Ϸ���һ�����㣬��
�Ḻ�����Ϸ���һ�����㣬��![]() ��������ֵ��
��������ֵ��
��3�������߶Գ������Ƿ���ڵ�![]() ��ʹ
��ʹ![]() Ϊ���������Σ������ڣ���ֱ��д������
Ϊ���������Σ������ڣ���ֱ��д������![]() ������꣬����������˵������.
������꣬����������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
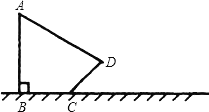
����Ŀ����ͼ�����߸�ABֱ���ڵ����ϣ�����Ӱ��ǡ���������µ�����CD�͵���BC�ϣ���CD������45�㣬��A��60�㣬CD��4m��![]() ������߸�AB�ij�Ϊ�����ף�
������߸�AB�ij�Ϊ�����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�Ϊ�������˿ͣ�����һ��������ת����ת�̣�����ͼ��3���������ڵ����������ȣ����涨���˿�ÿ����100Ԫ��Ʒ����ת������ת�̣�ת��ֹͣ��ָ��ָ������������ָ��ָ��ֽ��ߣ�������ת��ת�̣�ֱ��ָ��ָ����Ϊֹ�������ǣ���ָ�����ζ�ָ��3���˿Ϳɻ��90Ԫ����ȯ����ָ��ֻ��һ��ָ��3���˿Ϳɵ�36Ԫ����ȯ����ָ�����ζ���ָ��3���˿�ֻ�ܻ��18Ԫ����ȯ�����˿Ͳ�Ըת��ת�̣����ֱ�ӻ��30Ԫ����ȯ
��1��������״ͼ���б�����������ת��ת��ָ�����п���ָ��Ľ����
��2����ֱ���˿ͻ��90Ԫ��36Ԫ��18Ԫ����ȯ�ĸ��ʣ�
��3������Ϊת��ת�̺�ֱ�ӻ�ù���ȯ���ַ�ʽ�����㣿��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ǡ�ABC�У�BC��AB��AC������һ��P��ʹ�á�BPC���A�������ס������������ֱ����£�
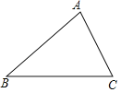
�ף���BΪԲ�ģ�AB��Ϊ�뾶������AC��P�㣬��P��Ϊ����.
�ң���BC�Ĵ�ֱƽ���ߺ͡�BAC��ƽ���ߣ����߽���P�㣬��P��Ϊ����.
���ڼס������˵�����������������ȷ����( )
A. ���˽���ȷB. ����ȷ���Ҵ���C. �״�������ȷD. ���˽Դ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
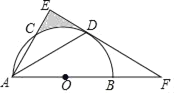
����Ŀ����ͼ��ABΪ��ԲO��ֱ����AC�ǡ�O��һ���ң�DΪ![]() ���е㣬��DE��AC����AB���ӳ����ڵ�F������DA��
���е㣬��DE��AC����AB���ӳ����ڵ�F������DA��
��1����֤��EFΪ��ԲO�����ߣ�
��2����DA��DF��6![]() ������Ӱ����������������������źͦУ�
������Ӱ����������������������źͦУ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���BAC=90�㣬AB=2AC����A��2��0����B��0��4������C�ڵ�һ�����ڣ�˫����y=![]() ��x��0��������C������ABC��y������ƽ��m����λ���ȣ�ʹ��Aǡ������˫�����ϣ���m��ֵΪ________��
��x��0��������C������ABC��y������ƽ��m����λ���ȣ�ʹ��Aǡ������˫�����ϣ���m��ֵΪ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
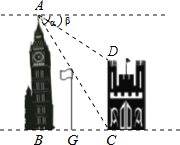
����Ŀ����ͼ������������֮����һ��ˣ���15�ף���A�㾭����˶���ǡ�ÿ������������ǽ��C�㣬�Ҹ�����Ϊ60�㣬�ִ�A����D��ĸ�����Ϊ30�㣬����˵ײ�G��ΪBC���е㣬������ĸ�CD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
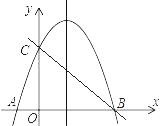
����Ŀ����ͼ��������y����x2+3x+4��x����A��B���㣨��A��B��ߣ�����y���ڵ�C��
��1����A��B��������ꣻ
��2����ֱ��BC�ĺ�����ϵʽ��
��3����P�������ߵĶԳ����ϣ�����PB��PC������PBC�����Ϊ4�����P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com