
【题目】如图,已知抛物线y=x2+bx+c与直线y=x交于(1,1)和(3,3)两点,现有以下结论:①b2﹣4c>0;②3b+c+6=0;③当x2+bx+c>![]() 时,x>2;④当1<x<3时,x2+(b﹣1)x+c<0,其中正确的序号是( )
时,x>2;④当1<x<3时,x2+(b﹣1)x+c<0,其中正确的序号是( )
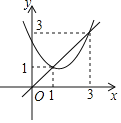
A. ①②④B. ②③④C. ②④D. ③④
【答案】C
【解析】
由函数y=x2+bx+c与x轴无交点,可得b2﹣4c<0;当x=3时,y=9+3b+c=3,3b+c+6=0;利用抛物线和双曲线交点(2,1)得出x的范围;当1<x<3时,二次函数值小于一次函数值,可得x2+bx+c<x,继而可求得答案.
∵函数y=x2+bx+c与x轴无交点,
∴b2﹣4ac<0;
∴b2﹣4c<0
故①不正确;
当x=3时,y=9+3b+c=3,
即3b+c+6=0;
故②正确;
把(1,1)(3,3)代入y=x2+bx+c,得抛物线的解析式为y=x2﹣3x+3,
当x=2时,y=x2﹣3x+3=1,y=![]() =1,
=1,
抛物线和双曲线的交点坐标为(2,1)
第一象限内,当x>2时,x2+bx+c>![]() ;
;
或第三象限内,当x<0时,x2+bx+c>![]() ;
;
故③错误;
∵当1<x<3时,二次函数值小于一次函数值,
∴x2+bx+c<x,
∴x2+(b﹣1)x+c<0.
故④正确;
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线系数”.
(1)任意抛物线都有“抛物线三角形”是______(填“真”或“假”)命题;
(2)若一条抛物线系数为[1,0,-2],则其“抛物线三角形”的面积为________;
(3)若一条抛物线系数为[-1,2b,0],其“抛物线三角形”是个直角三角形,求该抛物线的解析式;
(4)在(3)的前提下,该抛物线的顶点为A,与x轴交于O,B两点,在抛物线上是否存在一点P,过P作PQ⊥x轴于点Q,使得△BPQ∽△OAB,如果存在,求出P点坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣![]() x+c经过A(﹣2,0),B(0,2)两点,动点P,Q同时从原点出发均以1个单位/秒的速度运动,动点P沿x轴正方向运动,动点Q沿y轴正方向运动,连接PQ,设运动时间为t秒
x+c经过A(﹣2,0),B(0,2)两点,动点P,Q同时从原点出发均以1个单位/秒的速度运动,动点P沿x轴正方向运动,动点Q沿y轴正方向运动,连接PQ,设运动时间为t秒
(1)求抛物线的解析式;
(2)当BQ=![]() AP时,求t的值;
AP时,求t的值;
(3)随着点P,Q的运动,抛物线上是否存在点M,使△MPQ为等边三角形?若存在,请求出t的值及相应点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
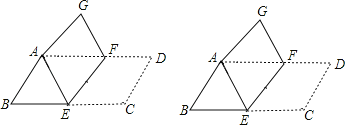
【题目】如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处.
(1)连接CF,求证:四边形AECF是菱形;
(2)若E为BC中点,BC=26,tan∠B=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
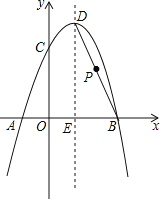
【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线对称轴DE交x轴于点E,连接BD.
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为 .
问题探究
(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
问题解决
(3)如图③所示,AB、AC、BC是某新区的三条规划路其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F.也就是,分别在![]() 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).
、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).



图① 图② 图③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某种品牌的篮球架实物图与示意图,已知底座BC=0.6米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.5米,篮板顶端F点到篮框D的距离FD=1.4米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离.(精确到0.1米.参考数据:cos75°≈0.3,sin75°≈0.9,.tan75°≈3.7,![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
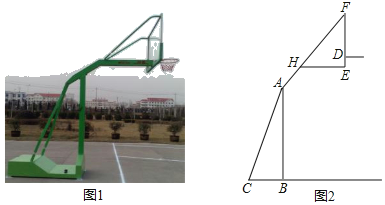
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=![]() (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b﹣![]() >0的解集.
>0的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙P的圆心是(2,a),半径为2,直线y=﹣x与⊙P相交于A、B两点,若弦AB的长为2![]() ,则a的值是( )
,则a的值是( )
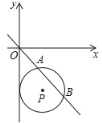
A. ﹣2![]() B. ﹣2+
B. ﹣2+![]() C. ﹣2﹣
C. ﹣2﹣![]() D. ﹣2﹣
D. ﹣2﹣![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com