
【题目】老师在微信群发了这样一个图:以线段AB为边作正五边形ABCDE和正三角形ABG,连接AC、DG,交点为F,下列四位同学的说法不正确的是( )
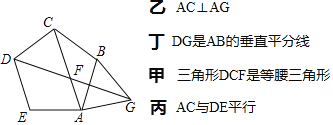
A. 甲B. 乙C. 丙D. 丁
 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
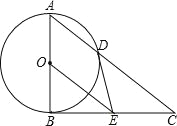
【题目】如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心、OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=2CD·OE;
(3)若cos∠BAD=![]() ,BE=6,求OE的长.
,BE=6,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将平行四边形纸片ABCD按如图方式折叠,使点C与点A重合,点D落到D’处,折痕为EF.
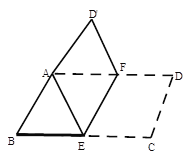
(1)、求证:△ABE≌△AD’F;
(2)、连接CF,判断四边形AECF是否为平行四边形?请证明你的结论。
(3)、若AE=5,求四边形AECF的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
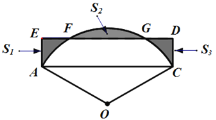
【题目】如图,半径为3的扇形AOB,∠AOB=120°,以AB为边作矩形ABCD交弧AB于点E,F,且点E,F为弧AB的四等分点,矩形ABCD与弧AB形成如图所示的三个阴影区域,其面积分别为![]() ,
,![]() ,
,![]() ,则
,则![]() 为( )(
为( )(![]() 取
取![]() )
)
A. ![]()
![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A,B两点(点A在点B左边),与y轴交于点C.
与x轴交于点A,B两点(点A在点B左边),与y轴交于点C.
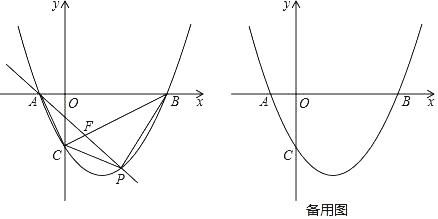
(1)求A,B两点的坐标.
(2)点P是线段BC下方的抛物线上的动点,连结PC,PB.
①是否存在一点P,使△PBC的面积最大,若存在,请求出△PBC的最大面积;若不存在,试说明理由.
②连结AC,AP,AP交BC于点F,当∠CAP=∠ABC时,求直线AP的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科研所计划建一幢宿舍楼,因为科研所实验中会产生辐射,所以需要有两项配套工程.①在科研所到宿舍楼之间修一条高科技的道路;②对宿含楼进行防辐射处理;已知防辐射费y万元与科研所到宿舍楼的距离xkm之间的关系式为y=ax+b(0≤x≤3).当科研所到宿舍楼的距离为1km时,防辐射费用为720万元;当科研所到宿含楼的距离为3km或大于3km时,辐射影响忽略不计,不进行防辐射处理,设修路的费用与x2成正比,且比例系数为m万元,配套工程费w=防辐射费+修路费.
(1)当科研所到宿舍楼的距离x=3km时,防辐射费y=____万元,a=____,b=____;
(2)若m=90时,求当科研所到宿舍楼的距离为多少km时,配套工程费最少?
(3)如果最低配套工程费不超过675万元,且科研所到宿含楼的距离小于等于3km,求m的范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学分别进行6次射击训练,训练成绩(单位:环)如下表
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六交 | |
甲 | 9 | 8 | 6 | 7 | 8 | 10 |
乙 | 8 | 7 | 9 | 7 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A. 他们训练成绩的平均数相同 B. 他们训练成绩的中位数不同
C. 他们训练成绩的众数不同 D. 他们训练成绩的方差不同
查看答案和解析>>
科目:初中数学 来源: 题型:
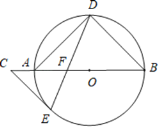
【题目】如图,AB是⊙O的直径,点D,E在⊙O上,∠B=2∠ADE,点C在BA的延长线上.
(Ⅰ)若∠C=∠DAB,求证:CE是⊙O的切线;
(Ⅱ)若OF=2,AF=3,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
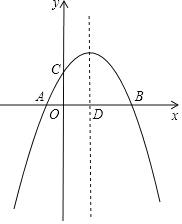
【题目】如图,抛物线y=ax2+![]() x+c(a≠0)与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知点A的坐标为(﹣1,0),点C的坐标为(0,2).
x+c(a≠0)与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知点A的坐标为(﹣1,0),点C的坐标为(0,2).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com