
【题目】为了美化环境,建设宜居城市,我市准备在一个广场上种植甲、乙两种花卉,经市场调查,甲种花卉的种植费用y(元)与种植面积x(m2)之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
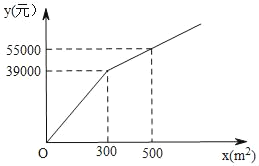
(1)试求出y与x的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共1200m2,若甲种花卉的种植面积不少于200m2,且不超过乙种花卉的种植面积的2倍.
①试求种植总费用W元与种植面积x(m2)之间的函数关系式;
②应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用W最少?最少总费用为多少元?
【答案】(1)y=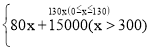 ;(2)①当200≤x≤300时,w=130x+100(1200-x)=30x+120000;当x>300时,w=80x+15000+100(1200-x)=-20x+135000;②应该分配甲、乙两种花卉的种植面积分别是800m2和400m2,才能使种植总费用最少,最少总费用为119000元.
;(2)①当200≤x≤300时,w=130x+100(1200-x)=30x+120000;当x>300时,w=80x+15000+100(1200-x)=-20x+135000;②应该分配甲、乙两种花卉的种植面积分别是800m2和400m2,才能使种植总费用最少,最少总费用为119000元.
【解析】
(1)由图可知y与x的函数关系式是分段函数,待定系数法求解析式即可.
(2)①根据(1)的结论解答即可;
②设甲种花卉种植为 am2,则乙种花卉种植(1200-a)m2,根据实际意义可以确定a的范围,结合种植费用w(元)与种植面积a(m2)之间的函数关系可以分类讨论最少费用为多少.
解:(1)当0≤x≤300时,设y=k1x,根据题意得300k1=39000,解得k1=130,即y=130x;
当x>300时,设y=k2x+b,根据题意得![]() ,解得
,解得![]() ,即y=80x+15000,
,即y=80x+15000,
∴y=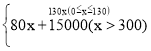 ;
;
(2)①当200≤x≤300时,w=130x+100(1200-x)=30x+120000;
当x>300时,w=80x+15000+100(1200-x)=-20x+135000;
②设甲种花卉种植为am2,则乙种花卉种植(1200-a)m2,
∴![]() ,
,
∴200≤a≤800
当a=200时.Wmin=126000 元
当a=800时,Wmin=119000 元
∵119000<126000
∴当a=800时,总费用最少,最少总费用为119000元.
此时乙种花卉种植面积为1200-800=400m2.
答:应该分配甲、乙两种花卉的种植面积分别是800m2和400m2,才能使种植总费用最少,最少总费用为119000元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E为![]() 的中点.
的中点.
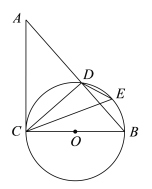
(1)求证:∠ACD=∠DEC;(2)延长DE、CB交于点P,若PB=BO,DE=2,求PE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
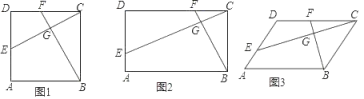
【题目】(1)如图1,正方形ABCD中,E、F分别是AD、DC边上的点,CE与BF交于点G,BF⊥CE,求证:BF=CE;
(2)如图2,矩形ABCD中,AB=2AD,E、F分别是AD、DC边上的点,CE与BF交于点G,∠A+∠BGE=180°,求证:CE=2BF;
(3)如图3,若(2)中的四边形ABCD是平行四边形,且∠A<90°,则CE=2BF是否仍然成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
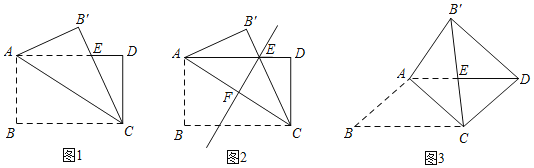
【题目】课题学习:矩形折纸中的数学实践操作:折纸不仅是一项有趣的活动,也是一项益智的数学活动.数学课上,老师给出这样一道题将矩形纸片ABCD沿对角线AC翻折,使点B落在矩形所在平面内,B'C和AD相交于点E,如图1所示.
探素发现:
(1)在图1中,①请猜想并证明AE和EC的数量关系;②连接B'D,请猜想并证明B'D和AC的位置关系;
(2)第1小组的同学发现,图1中,将矩形ABCD沿对角线AC翻折所得到的图形是轴对称图形.若沿对称轴EF再次翻折所得到的图形仍是轴对称图形,展开后如图2所示,请你直接写出该矩形纸片的长、宽之比;
(3)若将图1中的矩形变为平行四边形时(AB≠BC),如图3所示,(1)中的结论①和结论②是否仍然成立,请直接写出你的判断.
拓展应用:
(4)在图3中,若∠B=30°,AB=2,请您直接写出:当BC的长度为多少时,△AB'D恰好为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
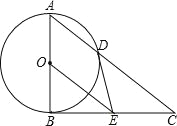
【题目】如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心、OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=2CD·OE;
(3)若cos∠BAD=![]() ,BE=6,求OE的长.
,BE=6,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问卷调查,调查结果为“A非常了解”、“B了解”、“C基本了解”三个等级,并根据调查结果制作了如下两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
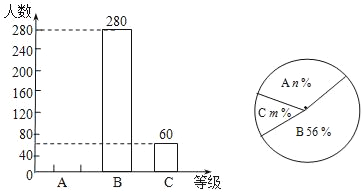
(1)本次调查的人数为 ;
(2)补全条形统计图;
(3)若该市约有市民100万人,请你根据抽样调查的结果,估计该市大约有多少人对“社会主义核心价值观”达到“A非常了解”的程度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了给游客提供更好的服务,某景区随机对部分游客进行了关于“景区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.
满意度 | 人数 | 所占百分比 |
非常满意 | 12 | 10% |
满意 | 54 | m |
比较满意 | n | 40% |
不满意 | 6 | 5% |

根据图表信息,解答下列问题:
(1)本次调查的总人数为______,表中m的值为_______;
(2)请补全条形统计图;
(3)据统计,该景区平均每天接待游客约3600人,若将“非常满意”和“满意”作为游客对景区服务工作的肯定,请你估计该景区服务工作平均每天得到多少名游客的肯定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科研所计划建一幢宿舍楼,因为科研所实验中会产生辐射,所以需要有两项配套工程.①在科研所到宿舍楼之间修一条高科技的道路;②对宿含楼进行防辐射处理;已知防辐射费y万元与科研所到宿舍楼的距离xkm之间的关系式为y=ax+b(0≤x≤3).当科研所到宿舍楼的距离为1km时,防辐射费用为720万元;当科研所到宿含楼的距离为3km或大于3km时,辐射影响忽略不计,不进行防辐射处理,设修路的费用与x2成正比,且比例系数为m万元,配套工程费w=防辐射费+修路费.
(1)当科研所到宿舍楼的距离x=3km时,防辐射费y=____万元,a=____,b=____;
(2)若m=90时,求当科研所到宿舍楼的距离为多少km时,配套工程费最少?
(3)如果最低配套工程费不超过675万元,且科研所到宿含楼的距离小于等于3km,求m的范围?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com