
����Ŀ����ͼ1����һ�������۵��������ϣ���A��B�ֱ��ʾ��-9��4.
(1)A��B����֮��ľ���Ϊ________.
(2)��ͼ2������Ե�CΪ�۵㣬�������������Ҷ��ۣ���ʱ��A���ڵ�B���ұ�1����λ���ȴ������C��ʾ������________.
(3)��ͼ1������A��ÿ��3����λ���ȵ��ٶ������������˶�����B��ÿ��2����λ���ȵ��ٶ�Ҳ�����������˶�����ô��������ʱ�䣬A��B�������4����λ����?

���𰸡�(1)13��(2)-2��(3)t= 9���17��.
��������
��1����������������ľ��빫ʽ������⣻
��2�����C��ʾ������x���ֱ��ʾ��AC��BC���ٸ���AC-BC=1�г����̽�ɣ�
��3���˶�t���֪��A��ʾ����Ϊ-9+3t����B��ʾ����Ϊ4+2t���ٸ���AB�ľ���Ϊ4���ɵ÷��̣��ⷽ�̼��ɣ�
�⣺��1��AB=4-��-9��=13
��2�����C��ʾ������x��
��AC=x-��-9��=x+9��BC=4-x��
��A���ڵ�B���ұ�1����λ��
��AC-BC=1,
��AC-BC=x+9-��4-x��=2x+5=1��
��ã�x=-2��
���C��ʾ������-2��
�ʴ�Ϊ��-2��
(3) ���˶�t���A���B���4����λ��
�������֪��A��ʾ����Ϊ-9+3t����B��ʾ����Ϊ4+2t��
��![]() ��
��
��![]() ��
��![]()
���t=17��9.
���˶�9���17���A���B���4����λ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������a��b���������㣺a��b��a��a+b����1����ʽ�ұ���ͨ���ļӷ����������˷����㣬���磬2��5��2����2+5����1��13������3���ѣ���5������3������3��5����1��23��
��1����2����3![]() ��ֵ��
��ֵ��
��2����������������m��n���������¶���һ�����㡰������ʹ��5��3��20��д���㶨������㣺m��n���� �����ú�m��n��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��һ���ڽ�Ϊ90�㣬�ҶԽ�����ȵ��ı��γ�Ϊ���Σ�
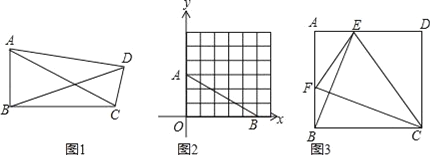
��1������ͼ1������ABCD�У���ABC=90�㣬��AB=2��BC=3����BD=�� ����
����ͼ2��ֱ������ϵ�У�A��0��3����B��5��0����������Pʹ���ı���AOBP�����Σ����P���������� ����������ָ�����ꡢ�����궼Ϊ�����ĵ㣩
��2����ͼ3��������ABCD�У���E��F�ֱ��DZ�AD��AB�ϵĵ㣬��CF��BE����֤���ı���BCEF�����Σ�
��3����֪������ABCD�У���ABC=90�㣬��BAC=60�㣬AB=2������ADCΪ����������ʱ����ֱ��д��������ε�������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=10cm��BC=15cm����P��A������AC��C����1����/����ٶ������ƶ�����Q��C������CB��B����2����/����ٶ������ƶ�����P��Q�ֱ�����ͬʱ�������ƶ���ijһλ��ʱ����ʱ��Ϊt��

��t = 4ʱ�����߶�PQ�ij���
(2)��tΪ��ֵʱ����PCQ�ǵ��������Σ�
��3����tΪ��ֵʱ����PCQ���������16cm2��
��4����tΪ��ֵʱ����PCQ�ס�ACB
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˷ֱ��A��B����ͬʱ������������У�����ǰ��B�ء�A�أ���������ʱͣ����4min���ָ���ԭ��ǰ��Ŀ�ĵأ��ס�������֮��ľ���y��m���������ʱ��x��min��֮��ĺ�����ϵ��ͼ��ʾ��������˵����

��A��B֮��ľ���Ϊ1200m�� �������ߵ��ٶ��Ǽ�1.5������ b=960�� �� a=34��
���Ͻ�����ȷ���У�������
A. �٢� B. �٢ڢ� C. �٢ۢ� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��![]() ��
��![]() ������������������
������������������![]() ��
��![]() ��
��![]() ��
��![]() �������������ƣ���
�������������ƣ���![]() ��ֵΪ�� ��
��ֵΪ�� ��
A.0B.-1C.1009D.-1009
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
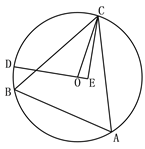
����Ŀ����ͼ����ABCΪ��O���ڽ������Σ�BC=24 , ![]() ,��DΪ��BC��һ���㣬CE��ֱֱ��OD�ڵ�E, ����D��B���ػ�BC�˶�����Cʱ����E������·����Ϊ�� ��
,��DΪ��BC��һ���㣬CE��ֱֱ��OD�ڵ�E, ����D��B���ػ�BC�˶�����Cʱ����E������·����Ϊ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С�ս�һ��������ֽƬ��ȥһ����Ϊ5cm�ij������ٴ�ʣ�µij�����ֽƬ�ϼ�ȥһ����Ϊ6cm�ij�����������μ��µij������������ȣ������������µij��������֮�ͣ�
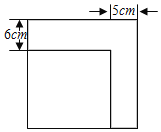
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У�BC=2AB��CE��AB��E��FΪAD���е㣬����AEF=54�����B=�� ��

A. 54 B. 60 C. 72 D. 66
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com