
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与
,与![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() ,且
,且![]() ,直线
,直线![]() 轴,在
轴,在![]() 轴上有一动点
轴上有一动点![]() 过点
过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() 与抛物线、直线
与抛物线、直线![]() 的交点分别为
的交点分别为![]() 、
、![]() .
.
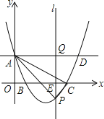
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 当
当![]() 时,求
时,求![]() 面积的最大值;
面积的最大值;
![]() 当
当![]() 时,是否存在点
时,是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出此时
相似?若存在,求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】![]()
![]() ;
;![]() 当
当![]() 时,
时,![]() 面积的最大值为
面积的最大值为![]() ;
;![]() 或
或![]() 或
或![]() .
.
【解析】
(1)由根与系数的关系可得![]() ,再由
,再由![]() 即可求得
即可求得![]() 、
、![]() ,所以
,所以![]() 、
、![]() ,把
,把![]() 代入
代入![]() 即可求得m的值,由此可得抛物线的解析式;(2)先求得点A的坐标,再用待定系数法求得直线AC的解析式,分当
即可求得m的值,由此可得抛物线的解析式;(2)先求得点A的坐标,再用待定系数法求得直线AC的解析式,分当![]() 时和当
时和当![]() 时两种情况求
时两种情况求![]() 得面积与t的函数关系式,根据二次函数的性质即可求得两种情况下
得面积与t的函数关系式,根据二次函数的性质即可求得两种情况下![]() 面积的最大值,比较即可解答;(3)分两种情况讨论:①当
面积的最大值,比较即可解答;(3)分两种情况讨论:①当![]() 时,
时,![]() ,
,![]() ,再由△AOB∽△AQP或△AOB∽△PQA,根据相似三角形的性质分别列出方程求解即可;②当
,再由△AOB∽△AQP或△AOB∽△PQA,根据相似三角形的性质分别列出方程求解即可;②当![]() 时,
时,![]() ,
,![]() ,再由△AOB∽△AQP或△AOB∽△PQA,根据相似三角形的性质分别列出方程求解即可.
,再由△AOB∽△AQP或△AOB∽△PQA,根据相似三角形的性质分别列出方程求解即可.
![]() 由题意知
由题意知![]() 、
、![]() 是方程
是方程![]() 的两根,
的两根,
∴![]() ,
,
由![]()
解得:![]()
∴![]() 、
、![]()
则![]() ,
,
解得:![]() ,
,
∴该抛物线解析式为:![]() ;
;
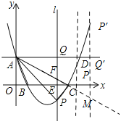
![]() 可求得
可求得![]()
设直线![]() 的解析式为:
的解析式为:![]() ,
,
∵![]()
∴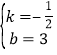
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
要构成![]() ,显然
,显然![]() ,分两种情况讨论:
,分两种情况讨论:
①当![]() 时,设直线
时,设直线![]() 与
与![]() 交点为
交点为![]() ,则:
,则:![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]()
![]()
![]()
![]() ,
,
此时最大值为:![]() ,
,
②当![]() 时,设直线
时,设直线![]() 与
与![]() 交点为
交点为![]() ,则:
,则:![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]()
![]()
![]() ,
,
当![]() 时,取最大值,最大值为:
时,取最大值,最大值为:![]() ,
,
综上可知,当![]() 时,
时,![]() 面积的最大值为
面积的最大值为![]() ;
;
![]() 如图,连接
如图,连接![]() ,则
,则![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
①当![]() 时,
时,![]() ,
,![]() ,
,
若:![]() ,则:
,则:![]() ,
,
即:![]() ,
,
∴![]() (舍),或
(舍),或![]() ,
,
若![]() ,则:
,则:![]() ,
,
即:![]() ,
,
∴![]() (舍)或
(舍)或![]() (舍),
(舍),
②当![]() 时,
时,![]() ,
,![]() ,
,
若:![]() ,则:
,则:![]() ,
,
即:![]() ,
,
∴![]() (舍),或
(舍),或![]() ,
,
若![]() ,则:
,则:![]() ,
,
即:![]() ,
,
∴![]() (舍)或
(舍)或![]() ,
,
∴![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知点P(3m-6,m+1),试分别根据下列条件,求出点P的坐标.
(1)点P的横坐标比纵坐标大1;
(2)点P在过点A(3,-2),且与x轴平行的直线上;
(3)点P到y轴的距离是到x轴距离的2倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某港口有一灯塔![]() ,灯塔
,灯塔![]() 的正东有
的正东有![]() 、
、![]() 两灯塔,以
两灯塔,以![]() 为直径的半圆区域内有若干暗礁,
为直径的半圆区域内有若干暗礁,![]() 海里,一船在
海里,一船在![]() 处测得灯塔
处测得灯塔![]() 、
、![]() 分别在船的
分别在船的
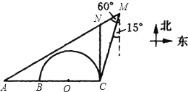
南偏西![]() 和南偏西
和南偏西![]() 方向,船沿
方向,船沿![]() 方向行驶
方向行驶![]() 海里恰好处在灯塔
海里恰好处在灯塔![]() 的正北方向
的正北方向![]() 处.
处.
![]() 求
求![]() 的长(精确到
的长(精确到![]() 海里);
海里);
![]() 若船继续沿
若船继续沿![]() 方向朝
方向朝![]() 行驶,是否有触礁的危险?
行驶,是否有触礁的危险?
(参考数值:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于某地供水管爆裂.该地供水部门组织工人进行抢修.供水部门距离抢修工地15千米.抢修车装载着所需材料先从供水部门出发,15分钟后,工人乘吉普车从同一地点出发,结果他们同时到达抢修工地.已知吉普车速度是抢修车速度的1.5倍,求这两种车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)已知二次函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象相交于
的图象相交于![]() ,
,![]() 且
且![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的值应满足( )
的值应满足( )
A. -3<x1<-2 B. -2<x1<-1 C. -1<x1<0 D. 0<x1<1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
如图,在△ABC中,点E、D、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.下列四个判断中,不正确的是( )
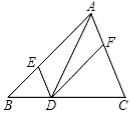
A.四边形AEDF是平行四边形
B.如果∠BAC=90°,那么四边形AEDF是矩形
C.如果AD平分∠BAC,那么四边形AEDF是矩形
D.如果AD⊥BC且AB=AC,那么四边形AEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(新知学习)
如果一个三角形有一边上的中线等于这条边的一半,那么我们就把这样的三角形叫做“智慧三角形”.
(简单运用)
(1)下列三个三角形,是智慧三角形的是______(填序号);

(2)如图,已知等边三角形![]() ,请用刻度尺在该三角形边上找出所有满足条件的点
,请用刻度尺在该三角形边上找出所有满足条件的点![]() ,使
,使![]() 为“智慧三角形”,并写出作法;
为“智慧三角形”,并写出作法;

(深入探究)
(3)如图,在正方形![]() 中,点
中,点![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 上一点,且
上一点,且![]() ,试判断
,试判断![]() 是否为“智慧三角形”,并说明理由;
是否为“智慧三角形”,并说明理由;

(灵活应用)
(4)如图,等边三角形![]() 边长
边长![]() .若动点
.若动点![]() 以
以![]() 的速度从点
的速度从点![]() 出发,沿
出发,沿![]() 的边
的边![]() 运动.若另一动点
运动.若另一动点![]() 以
以![]() 的速度从点
的速度从点![]() 出发,沿边
出发,沿边![]() 运动,两点同时出发,当点
运动,两点同时出发,当点![]() 首次回到点
首次回到点![]() 时,两点同时停止运动.设运动时间为
时,两点同时停止运动.设运动时间为![]() ,那么
,那么![]() 为______
为______![]() 时,
时,![]() 为“智慧三角形”.
为“智慧三角形”.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB、AC的垂直平分线分别交BC于点E、F.若△AEF的周长为12cm,则BC的长为____________________cm.若∠EAF=110°,则∠BAC=_____________________.
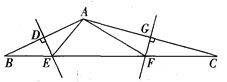
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E点.

(1)当∠BDA=115°时,∠BAD=___°,∠DEC=___°;
(2)当DC等于多少时,△ABD与△DCE全等?请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com