
分析 (1)根据绝对值的定义去绝对值即可求解,
(2)根据(1)中规律即可总结出答案,
(3)根据(2)中结论即可得出答案.
解答 解:(1)∵①|-2|+|3|=5,|-2+3|=1,
∴|-2|+|3|>|-2+3|,
∵②|-2|+|-3|=5,|(-2)+(-3)|=5,
∴|-2|+|-3|=|-2-3|,
∵③|0|+|-2|=2,|-2+0|=2,
∴|-2|+|0|=|-2+0|;
故答案为>,=,=,
(2)根据(1)中规律可得出:|a|+|b|≥|a+b|,
(3)∵|-2016|=2016,
∴|x|+2016=|x|+|-2016|=|x+(-2016)|=|x-2016|,
∴x≤0,
即:当|x|+2016=|x-2016|时,x≤0.
点评 此题考查了有理数的加法,熟练掌握运算法则是解本题的关键.


 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
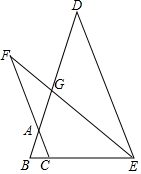 如图,在△ABC中,AB=AC,点D、E、F为三边延长线上的点,且DE∥AC,连接EF交BD于点G,∠BEF+2∠B=180°.
如图,在△ABC中,AB=AC,点D、E、F为三边延长线上的点,且DE∥AC,连接EF交BD于点G,∠BEF+2∠B=180°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,数轴上A,B两点表示的数分别为-1,-$\sqrt{2}$,点B关于点A的对称点为点C,则点C所表示的数是( )
如图,数轴上A,B两点表示的数分别为-1,-$\sqrt{2}$,点B关于点A的对称点为点C,则点C所表示的数是( )| A. | 1-$\sqrt{2}$ | B. | $\sqrt{2}$-1 | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}$-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 60 | B. | 30 | C. | 240 | D. | 120 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com