
【题目】请认真观察图形,解答下列问题:
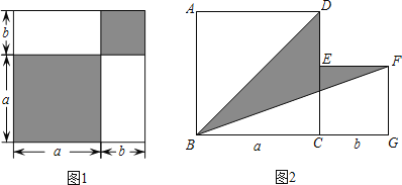
(1)根据图1中条件,试用两种不同方法表示两个阴影图形的面积的和.
方法1:______;
方法2:______.
(2)从中你能发现什么结论?请用等式表示出来:______;
(3)利用(2)中结论解决下面的问题:
如图2,两个正方形边长分别为a、b,如果a+b=ab=4,求阴影部分的面积.
【答案】(1)a2+b2,(a+b)2-2ab;(2)a2+b2=(a+b)2-2ab;(3)阴影部分的面积=2.
【解析】
(1)方法1:两个正方形面积和,方法2:大正方形面积-两个小长方形面积;
(2)由题意可直接得到;
(3)由阴影部分面积=正方形ABCD的面积+正方形CGFE的面积-三角形ABD的面积-三角形BGF的面积,可求阴影部分的面积.
解:(1)由题意可得:方法1:a2+b2 方法2:(a+b)2-2ab,
故答案为:a2+b2,(a+b)2-2ab;
(2)a2+b2=(a+b)2-2ab,
故答案为:a2+b2=(a+b)2-2ab;
(3)∵阴影部分的面积=S正方形ABCD+S正方形CGFE-S△ABD-S△BGF=a2+b2-![]() a2-
a2-![]() (a+b)b
(a+b)b
∴阴影部分的面积=![]() a2+
a2+![]() b2-
b2-![]() ab=
ab=![]() [(a+b)2-2ab]-
[(a+b)2-2ab]-![]() ab,
ab,
∵a+b=ab=4,
∴阴影部分的面积=![]() [(a+b)2-2ab]-
[(a+b)2-2ab]-![]() ab=2.
ab=2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过点G作GE⊥AD于点E.若AB=2,且∠1=∠2,则下列结论:①DF⊥AB;②CG=2GA;③CG=DF+GE;④S四边形BFOC=![]() .其中正确的有( )
.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
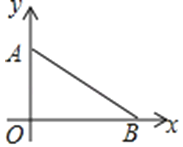
【题目】如图,在平面直角坐标系中,点A在x轴上,坐标为(0,3),点B在x轴上.
(1)在坐标系中求作一点M,使得点M到点A,点B和原点O这三点的距离相等,在图中保留作图痕迹,不写作法;
(2)若sin∠OAB=![]() ,求点M的坐标.
,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
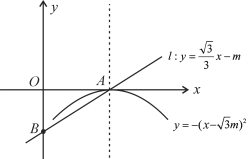
【题目】如图所示,抛物线![]() (m>0)的顶点为A,直线
(m>0)的顶点为A,直线![]() 与
与![]() 轴的交点为点B.
轴的交点为点B.
(1)求出抛物线的对称轴及顶点A的坐标(用含![]() 的代数式表示);
的代数式表示);
(2)证明点A在直线![]() 上,并求∠OAB的度数;
上,并求∠OAB的度数;
(3)动点Q在抛物线对称轴上,问:抛物线上是否存在点P,使以点P、Q、A为顶点的三角形与△OAB全等?若存在,求出![]() 的值,并写出所有符合上述条件的点P的坐标;若不存在,请说明理由.
的值,并写出所有符合上述条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-2x)(x2-2x+2)+1进行因式分解的过程:
解:设x2-2x=y
原式=y (y+2)+1 (第一步)
=y2+2y+1 (第二步)
=(y+1)2 (第三步)
=(x2-2x+1)2 (第四步)
请问:
(1)该同学因式分解的结果是否彻底? (填“彻底”或“不彻底”),若不彻底,则该因式分解的最终结果为 ;
(2)请你模仿上述方法,对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;②AE=AF;③∠EBC=∠C;④FG∥AC;⑤EF=FG.其中正确的结论是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需要粉刷一些相同的房间,经调查3名师傅一天粉刷8个房间,还剩40m2刷不完;5名徒弟一天可以粉刷9个房间;每名师傅比徒弟一天多刷30m2的墙面。
(1)求每个房间需要粉刷的面积;
(2)该公司现有36个这样的房间需要粉刷,若只聘请1名师傅和2名徒弟一起粉刷,需要几天完成?
(3)若来该公司应聘的有3名师傅和10名徒弟,每名师傅和每名徒弟每天的工资分别是240元和200元,该公司要求这36个房间要在2天内粉刷完成,问人工费最低是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com