练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

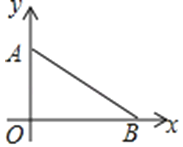
    【题目】如图，在平面直角坐标系中，点A在x轴上，坐标为（0，3），点B在x轴上．

    （1）在坐标系中求作一点M，使得点M到点A，点B和原点O这三点的距离相等，在图中保留作图痕迹，不写作法；

    （2）若sin∠OAB=，求点M的坐标．

    【答案】(1)作图见解析；（2）（2，）．

    【解析】整体

    （1）直角三角形斜边上的中点到三个顶点的距离相等；（2）根据OA=3，sin∠OAB=求出B的坐标，再由M是AB的中点，求点M的坐标.

    解：（1）如图所示：点M，即为所求；

    （2）∵sin∠OAB=，

    ∴设OB=4x，AB=5x，

    由勾股定理可得：32+（4x）2=（5x）2，

    解得：x=1，

    ∴OB=4，由B（4，0），

    由作图可得：M为AB的中点，则M的坐标为：（2，）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图所示，在△ABC中，∠BAC的平分线AD交BC于点D，DE垂直平分AC，垂足为点E，∠BAD=29°，求∠B的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某烤鸭店在确定烤鸭的烤制时间时，主要依据的是下表的数据：

    鸭的质量/千克

    0.5

    1

    1.5

    2

    2.5

    3

    3.5

    4

    烤制时间/分

    40

    60

    80

    100

    120

    140

    160

    180

    设鸭的质量为x千克，烤制时间为t，估计当x=2.8千克时，t的值为（ ）

    A. 128B. 132C. 136D. 140

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校运动会需购买A、B两种奖品共100件、B两种奖品单价分别为10元、15元设购买A种奖品m件，购买两种奖品的总费用为W元．

    写出元与件之间的函数关系式；

    若购买两种奖品的总费用不超过1150元，且A种奖品的数量不大于B种奖品数量的3倍，求出自变量m的取值范围，并确定最少费用W的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在半径为6cm的⊙O中，点A是劣弧BC的中点，点D是优弧BC上一点，且∠D＝30°，下列四个结论：①OA⊥BC；②BC＝6cm；③sin∠AOB＝；④四边形ABOC是菱形．其中正确结论的序号是（ ）

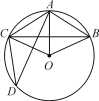
    A. ①③ B. ①②③④ C. ②③④ D. ①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形连接AC交EF于G，下列结论: ①BE＝DF，②∠DAF＝15°，③AC⊥EF，④BE+DF＝EF，⑤EC＝FG；其中正确结论有( )个

    A.2B.3C.4D.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知EF∥AD，∠1＝∠2，∠BAC＝70°，求∠AGD（请填空）

    解：∵EF∥AD

    ∴∠2＝　 　（　 　

    又∵∠1＝∠2

    ∴∠1＝∠3（　 　）

    ∴AB∥　 　（　 　）

    ∴∠BAC+　 　＝180°（　 　）

    ∵∠BAC＝70°（　 　）

    ∴∠AGD＝　 　（　 　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

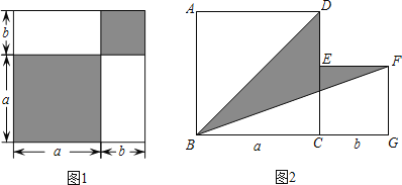
    【题目】请认真观察图形，解答下列问题：

    （1）根据图1中条件，试用两种不同方法表示两个阴影图形的面积的和．

    方法1：______；

    方法2：______．

    （2）从中你能发现什么结论？请用等式表示出来：______；

    （3）利用（2）中结论解决下面的问题：

    如图2，两个正方形边长分别为a、b，如果a+b=ab=4，求阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

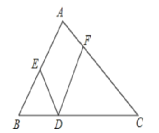
    【题目】如图所示，在△ABC中，点D. E. F分别在BC、AB、AC上，且BD=BE，CD=CF，∠EDF=50°.则∠A的度数为___________．

    查看答案和解析>>

    同步练习册答案