
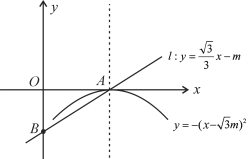
【题目】如图所示,抛物线![]() (m>0)的顶点为A,直线
(m>0)的顶点为A,直线![]() 与
与![]() 轴的交点为点B.
轴的交点为点B.
(1)求出抛物线的对称轴及顶点A的坐标(用含![]() 的代数式表示);
的代数式表示);
(2)证明点A在直线![]() 上,并求∠OAB的度数;
上,并求∠OAB的度数;
(3)动点Q在抛物线对称轴上,问:抛物线上是否存在点P,使以点P、Q、A为顶点的三角形与△OAB全等?若存在,求出![]() 的值,并写出所有符合上述条件的点P的坐标;若不存在,请说明理由.
的值,并写出所有符合上述条件的点P的坐标;若不存在,请说明理由.
【答案】(1)抛物线的对称轴为直线![]() ,顶点A的坐标为(
,顶点A的坐标为(![]() ,0);(2)∠OAB=30°;(3)存在,①
,0);(2)∠OAB=30°;(3)存在,①![]() =
=![]() 时, P
时, P![]() (0,-
(0,-![]() ),P
),P![]() (
(![]() ,-
,-![]() );②
);②![]() =
=![]() 时,P
时,P![]() (
(![]() ,-3),P
,-3),P![]() (3+
(3+![]() ,-3);③
,-3);③![]() =2时, P
=2时, P![]() (
(![]() ,-3),P
,-3),P![]() (
(![]() ,-3);④
,-3);④![]() =
=![]() 时, P
时, P![]() (
(![]() ,-
,-![]() ),P
),P![]() (
(![]() ,-
,-![]() ).
).
【解析】(1)根据抛物线的解析式可得出抛物线的对称轴和A点坐标,
(2)将A点坐标代入直线的解析式中进行验证即可得出A点是否在直线y=![]() xm上的.求∠OAB的度数,可通过求∠OAB的正切值来得出,根据直线AB的解析式可得出B点坐标,即可得出OB的长,OA的长已求出,因此可在三角形OAB中得出∠OAB的正切值.即可得出∠OAB的度数.
xm上的.求∠OAB的度数,可通过求∠OAB的正切值来得出,根据直线AB的解析式可得出B点坐标,即可得出OB的长,OA的长已求出,因此可在三角形OAB中得出∠OAB的正切值.即可得出∠OAB的度数.
(3)本题可分成四种情况:
一:∠AQP=∠AOB=90°:
①AO=PQ,OB=AQ,此时P、B重合,即可求出P点坐标(根据抛物线的对称性可知:P点关于抛物线对称轴的对称点也符合要求).
②AO=AQ,PQ=OB,此时P点纵坐标的绝对值与A点横坐标相等,可将其代入抛物线的解析式中,可得出两个符合条件的P点坐标.
二:∠APQ=∠AOB=90°:
①AO=PA,OB=PQ,可过P作抛物线对称轴的垂线,通过∠PAQ的度数和AP即OA的长求出P点纵坐标,然后代入抛物线的解析式中即可得出两个符合条件的P点坐标.
②AO=PQ,PA=OB,同①
因此本题共有8个符合条件的P点坐标.
(1)对称轴:x=![]() m;
m;
顶点:A(![]() m,0).
m,0).
(2)将x=![]() m代入函数y=
m代入函数y=![]() x-m,
x-m,
得y=![]() ×
×![]() m-m=0
m-m=0
∴点A(![]() m,0)在直线l上.
m,0)在直线l上.
当x=0时,y=-m,
∴B(0,-m)
tan∠OAB=![]() ,
,
∴∠OAB=30度.
(3)以点P、Q、A为顶点的三角形与△OAB全等共有以下四种情况:
①当∠AQP=90°,PQ=![]() m,AQ=m时,
m,AQ=m时,
如图1,此时点P在y轴上,与点B重合,其坐标为(0,-m),


代入抛物线y=-(x-![]() m)2
m)2
得-m=-3m2,
∵m>0,
∴m=![]()
这时有P1(0,-![]() )
)
其关于对称轴的对称点P2(![]() ,-
,- ![]() )也满足条件.
)也满足条件.
②当∠AQP=90°,PQ=m,AQ=![]() m时
m时
点P坐标为(![]() m-m,-
m-m,-![]() m),
m),
代入抛物线y=-(x-![]() m)2
m)2
得![]() m=m2,
m=m2,
∵m>0,
∴m=![]()
这时有P3(3-![]() ,-3)
,-3)
还有关于对称轴的对称点P4(3+![]() ,-3).
,-3).
③当∠APQ=90°,AP=![]() m,PQ=m时
m,PQ=m时
点P坐标为(![]() m,
m,![]() m),代入抛物线y=-(x-
m),代入抛物线y=-(x-![]() m)2
m)2
得![]() m=
m=![]() m2,
m2,
∵m>0,
∴m=2
这时有P5(![]() ,-3)
,-3)
还有关于对称轴的对称点P6(3![]() ,-3).
,-3).

④当∠APQ=90°,AP=m,PQ=![]() m时
m时
点P坐标为(![]() m,
m,![]() m),
m),
代入抛物线y=-(x-![]() m)2
m)2
得![]() m=
m=![]() m2,
m2,
∵m>0,
∴m=![]()
这时有P7(![]() ,-
,-![]() )
)
还有关于对称轴对称的点P8(![]() ,-
,-![]() ).
).
所以当m=![]() 时,有点P1(0,-
时,有点P1(0,-![]() ),P2(
),P2(![]() ,-
,-![]() );
);
当m=![]() 时,有点P3(3-
时,有点P3(3-![]() ,-3),P4(3+
,-3),P4(3+![]() ,-3);
,-3);
当m=2时,有点P5(![]() ,-3),P6(3
,-3),P6(3![]() ,-3);
,-3);
当m=![]() 时,有点P7(
时,有点P7(![]() ,-
,-![]() ),P8(
),P8(![]() ,-
,-![]() ).
).


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于点C,连接AD,OC.若△ABO的周长为
的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于点C,连接AD,OC.若△ABO的周长为![]() ,AD=2,则△ACO的面积为_________.
,AD=2,则△ACO的面积为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形连接AC交EF于G,下列结论: ①BE=DF,②∠DAF=15°,③AC⊥EF,④BE+DF=EF,⑤EC=FG;其中正确结论有( )个

A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于未知数为 x,y 的二元一次方程组,如果方程组的解 x,y 满足![]() ,我们就说方程组的解 x 与 y 具有“邻好关系”.
,我们就说方程组的解 x 与 y 具有“邻好关系”.
(1) 方程组![]() 的解x与y是否具有“邻好关系”? 说明你的理由;
的解x与y是否具有“邻好关系”? 说明你的理由;
(2) 若方程组![]() 的解x与y具有“邻好关系”,求m的值;
的解x与y具有“邻好关系”,求m的值;
(3) 未知数为x,y的方程组![]() ,其中a与x,y都是正整数,该方程组的解x与y是否具有“邻好关系”? 如果具有,请求出a的值及方程组的解;如果不具有,请说明理由.
,其中a与x,y都是正整数,该方程组的解x与y是否具有“邻好关系”? 如果具有,请求出a的值及方程组的解;如果不具有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
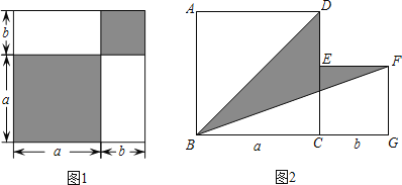
【题目】请认真观察图形,解答下列问题:
(1)根据图1中条件,试用两种不同方法表示两个阴影图形的面积的和.
方法1:______;
方法2:______.
(2)从中你能发现什么结论?请用等式表示出来:______;
(3)利用(2)中结论解决下面的问题:
如图2,两个正方形边长分别为a、b,如果a+b=ab=4,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在以线段AB为直径的⊙O上取一点,连接AC、BC.将△ABC沿AB翻折后得到△ABD.
(1)试说明点D在⊙O上;
(2)在线段AD的延长线上取一点E,使AB2=AC·AE.求证:BE为⊙O的切线;
(3)在(2)的条件下,分别延长线段AE、CB相交于点F,若BC=2,AC=4,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系xOy 中,抛物线y=ax2+bx+3经过点A(-1,0) 、B(3,0) 两点,且与y轴交于点C
.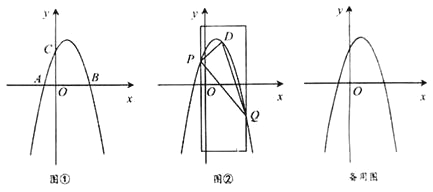
(1)求抛物线的表达式;
(2)如图②,用宽为4个单位长度的直尺垂直于x轴,并沿x轴左右平移,直尺的左右两边所在的直线与抛物线相交于P、 Q两点(点P在点Q的左侧),连接PQ,在线段PQ上方抛物线上有一动点D,连接DP、DQ.
①若点P的横坐标为![]() ,求△DPQ面积的最大值,并求此时点D 的坐标;
,求△DPQ面积的最大值,并求此时点D 的坐标;
②直尺在平移过程中,△DPQ面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年5月3日,中国科学院在上海发布了中国首款人工智能芯片:寒武纪(MLU100),该芯片在平衡模式下的等效理论峰值速度达每秒128 000 000 000 000次定点运算,将数
128 000 000 000 000用科学计数法表示为( )
A. 1.28![]() 1014 B. 1.28
1014 B. 1.28![]() 10-14 C. 128
10-14 C. 128![]() 1012 D. 0.128
1012 D. 0.128![]() 1011
1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数![]() 的图象上,从左向右第3个正方形中的一个顶点A的坐标为
的图象上,从左向右第3个正方形中的一个顶点A的坐标为![]() ,阴影三角形部分的面积从左向右依次记为
,阴影三角形部分的面积从左向右依次记为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() 的值为______
的值为______![]() 用含n的代数式表示,n为正整数
用含n的代数式表示,n为正整数![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com