【题目】2018年5月3日，中国科学院在上海发布了中国首款人工智能芯片：寒武纪（MLU100），该芯片在平衡模式下的等效理论峰值速度达每秒128 000 000 000 000次定点运算，将数
128 000 000 000 000用科学计数法表示为（ ）
A. 1.28
1014 B. 1.2810-14 C. 1281012 D. 0.1281011
科目：初中数学 来源： 题型：
【题目】如图，抛物线y＝－
x2－
x＋
与x轴交于A、B两点（点A在点B的左侧），与y轴于点C，已知点D(0，－)．
（1）求直线AC的解析式；
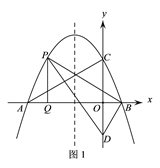
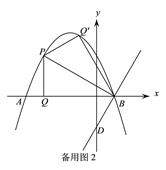
（2）如图1，P为直线AC上方抛物线上的一动点，当△PBD的面积最大时，过P作PQ⊥x轴于点Q，M为抛物线对称轴上的一动点，过M作y轴的垂线，垂足为点N，连接PM、NQ，求PM＋MN＋NQ的最小值；
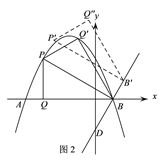
（3）在（2）问的条件下，将得到的△PBQ沿PB翻折得到△PBQ′，将△PBQ′沿直线BD平移，记平移中的△PBQ′为△P′B′Q″，在平移过程中，设直线P′B′与x轴交于点E，则是否存在这样的点E，使得△B′EQ″为等腰三角形？若存在，求此时OE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知点B，E，C，F在一条直线上，AC∥DE，∠A=∠D，AB=DF．
（1）试说明：△ABC≌△DFE；
（2）若BF=13，EC=7，求BC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（3分）如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE=2BF．给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AC=3BF，其中正确的结论共有（ ）
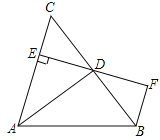
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在边长为a的正方形的一角剪去一个边长为b的正方形，把剩余的部分（图中的阴影部分）裁剪后拼成右边的长方形．
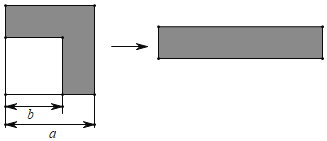
（1）请写出上述剪拼过程中所揭示的乘法公式；
（2）请运用乘法公式简便计算：20192﹣2020×2018．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，M、N、C三点的坐标分别为（
，1），（3，1），（3，0），点A为线段MN上的一个动点，连接AC，过点A作
交y轴于点B，当点A从M运动到N时，点B随之运动，设点B的坐标为（0，b），则b的取值范围是（ ）
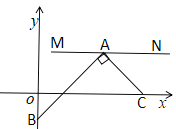
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明在一条笔直的公路进行跑步训练，可以用如图所示一条直线上来刻画他在公路上跑步情境．假定向右跑步的路程记为正数，向左跑步的路程记为负数，则所跑步的各段路程依次记为：+5，-3，-6，+8，-6，+12，-10．(单位：百米)
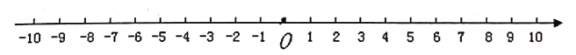
（1）小明最后是否回到出发点
?
（2）小明在跑步过程中距离出发点最远是多少米?．
（3）在跑步过程中，如果小明每跑1千米会消耗约60卡热量，那么小明此次训练一共会消耗多少卡?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,已知：∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为( )
A. 16B. 32C. 64D. 128
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某自行车厂计划一周生产自行车1400辆，平均每天生产200辆，但由于种种原因，实际每天生产量与计划量相比有出入，下表是某周的生产情况（超产记为正、减产记为负）：
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
增减产值 |
|
|
|
|
|
|
|
（1）根据记录的数据可知该厂星期五生产自行车__________辆．
（2）根据记录的数据可知该厂本周实际生产自行车_________辆．
（3）该厂实行每日计件工资制，每生产一辆车可得60元，若超额完成任务，则超过部分每辆另奖15元，若没有完成任务，少生产一辆扣20元，那么该厂工人这一周的工作总额是多少元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
