
【题目】某公司需要粉刷一些相同的房间,经调查3名师傅一天粉刷8个房间,还剩40m2刷不完;5名徒弟一天可以粉刷9个房间;每名师傅比徒弟一天多刷30m2的墙面。
(1)求每个房间需要粉刷的面积;
(2)该公司现有36个这样的房间需要粉刷,若只聘请1名师傅和2名徒弟一起粉刷,需要几天完成?
(3)若来该公司应聘的有3名师傅和10名徒弟,每名师傅和每名徒弟每天的工资分别是240元和200元,该公司要求这36个房间要在2天内粉刷完成,问人工费最低是多少?
【答案】(1)50 m2;(2)6天;(3)3840元.
【解析】
(1)可利用“每个房间需要粉刷的墙面面积”作为相等关系列方程求出徒弟和师傅的工作效率,再代入求每个房间需要粉刷的墙面面积;
(2)直接利用工作总量除以工作效率可求出工作时间;
(3)根据师傅与徒弟的工资以及工作效率分别分析得出即可.
(1)设每名徒弟一天粉刷的面积为xm2,师傅为(x+30)m2,
![]()
解得:x=90,所以每个房间需要粉刷的墙面面积为![]() 平方米.
平方米.
答:每个房间需要粉刷的墙面面积为50平方米.
(2)由(1)可知每名徒弟一天粉刷的面积为90m2,师傅为120m2,则![]() 天.
天.
答:若请1名师傅带2名徒弟去,需要6天完成.
(3)一个师傅每天刷120㎡,需要240元钱,所以师傅每刷1平方米需要2元钱,
徒弟每天刷90㎡,需要200元钱,所以徒弟每刷1平方米需要![]() 元钱,
元钱,
所以刷同样的面积师傅的工费较低,
故先请3名师傅干两天,可刷墙3×2×120=720㎡,人工3×2×240=1440元,
剩下的36×50-720=1080㎡,需要徒弟完成,需要徒弟人次为1080÷90=12,故雇佣6名徒弟干两天,需要花费6×2×200=2400元,所以总花费1440+2400=3840元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
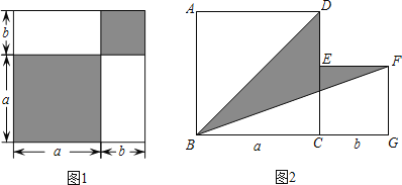
【题目】请认真观察图形,解答下列问题:
(1)根据图1中条件,试用两种不同方法表示两个阴影图形的面积的和.
方法1:______;
方法2:______.
(2)从中你能发现什么结论?请用等式表示出来:______;
(3)利用(2)中结论解决下面的问题:
如图2,两个正方形边长分别为a、b,如果a+b=ab=4,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
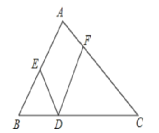
【题目】如图所示,在△ABC中,点D. E. F分别在BC、AB、AC上,且BD=BE,CD=CF,∠EDF=50°.则∠A的度数为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
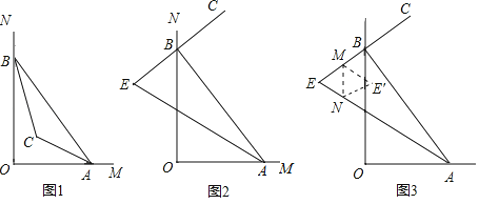
【题目】已知∠MON=90°,点A,B分别在射线OM,ON上运动(不与点O重合),
观察:
(1)如图1,若∠OBA和∠OAB的平分线交于点C,∠ACB= °
猜想:
(2)如图2,随着点A,B分别在射线OM,ON上运动(不与点O重合).若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点E,∠E的大小会变吗?如果不会,求∠E的度数;如果会改变,说明理由.
拓展:
(3)如图3,在(2)基础上,小明将△ABE沿MN折叠,使点E落在四边形ABMN内点E′的位置.求∠BME′+∠ANE′的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列有四个结论,其中正确的是( )
①若x 1![]() 1,则 x 只能是 2;
1,则 x 只能是 2;
②若x 1x![]() ax 1的运算结果中不含 x
ax 1的运算结果中不含 x![]() 项,则 a=1;
项,则 a=1;
③若2x 4 ![]() - 2x - 3
- 2x - 3![]() 有意义,则 x 的取值范围是 x 2 ;
有意义,则 x 的取值范围是 x 2 ;
④若 4![]() a,8
a,8![]() b,则2
b,则2![]() 可表示为
可表示为![]()
A.②④B. ②③④C. ①③④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数![]() 的图象上,从左向右第3个正方形中的一个顶点A的坐标为
的图象上,从左向右第3个正方形中的一个顶点A的坐标为![]() ,阴影三角形部分的面积从左向右依次记为
,阴影三角形部分的面积从左向右依次记为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() 的值为______
的值为______![]() 用含n的代数式表示,n为正整数
用含n的代数式表示,n为正整数![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列段文字,再解答问题:
已知在平面内有两点![]() 其两点间的距离公式为:
其两点间的距离公式为:
![]()
(1)已知点P(2,4)、Q(-3,-8),试求P、Q两点间的距离;
(2)已知点A(0,6)、B(-3,2)、C(3,2),判断线段AB、BC、AC中哪两条线段是相等的?并说明理由;
(3)已知点![]() 且MN=10,求
且MN=10,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+4与x轴、y轴分别交于点A、B、C是线段AB上一点,四边形OADC是菱形,则OD的长为( )
x+4与x轴、y轴分别交于点A、B、C是线段AB上一点,四边形OADC是菱形,则OD的长为( )
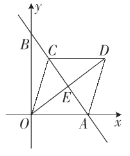
A. 4.2B. 4.8C. 5.4D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决线段数量关系问题中,如果条件中有角平分线,经常采用下面构造全等三角形的解决思路.如:在图1中,若![]() 是
是![]() 的平分线
的平分线![]() 上一点,点
上一点,点![]() 在
在![]() 上,此时,在
上,此时,在![]() 截取
截取![]() ,连接
,连接![]() ,根据三角形全等的判定
,根据三角形全等的判定![]() ,容易构造出全等三角形⊿
,容易构造出全等三角形⊿![]() 和⊿
和⊿![]() ,参考上面的方法,解答下列问题:
,参考上面的方法,解答下列问题:

如图2,在非等边⊿![]() 中,
中, ![]() ,
, ![]() 分别是
分别是![]() 的平分线,且
的平分线,且![]() 交于点
交于点![]() .求证:
.求证: ![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com