
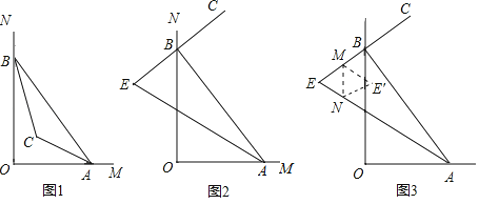
【题目】已知∠MON=90°,点A,B分别在射线OM,ON上运动(不与点O重合),
观察:
(1)如图1,若∠OBA和∠OAB的平分线交于点C,∠ACB= °
猜想:
(2)如图2,随着点A,B分别在射线OM,ON上运动(不与点O重合).若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点E,∠E的大小会变吗?如果不会,求∠E的度数;如果会改变,说明理由.
拓展:
(3)如图3,在(2)基础上,小明将△ABE沿MN折叠,使点E落在四边形ABMN内点E′的位置.求∠BME′+∠ANE′的度数.
【答案】观察:(1)135.猜想:(2)∠E=45°.拓展:(3)90°.
【解析】
(1)根据三角形内角和定理得到∠OBA+∠OAB=90°,根据角平分线的定义计算即可;
(2)根据角平分线的定义再进行等量代换,计算即可;
(3)根据折叠的性质得到∠BM E′+∠ANE′=360°﹣2(∠EMN+∠ENM),根据三角形内角和定理计算即可
解:(1)∵∠MON=90°,
∴∠OAB+∠OBA=90°,
∵∠OBA和∠OAB的平分线交于点C,
∴∠ABC=![]() ∠OBA,∠BAC=
∠OBA,∠BAC=![]() ∠OAB,
∠OAB,
∴∠ABC+∠BAC=![]() (∠OBA+∠OAB)=45°,
(∠OBA+∠OAB)=45°,
∴∠CBA=180°﹣45°=135°
故答案为135.
(2)∵AE是∠BAO的平分线
∴∠BAE=![]() ∠BAO,
∠BAO,
∵BC是∠ABN的平分线,
∴∠CBA=![]() ∠NBA,
∠NBA,
∵∠NBA=∠O+∠BAO,
∴∠CBA=![]() (∠O+∠BAO)=45°+∠BAE,
(∠O+∠BAO)=45°+∠BAE,
∵∠CBA=∠E+∠BAE,
∴∠E+∠BAE=45°+∠BAE,
即∠E=45°.
(3)由折叠可得,∠EMN=∠E′MN,∠E N M=∠E′NM,
∴2∠EMN+∠BM E′=180°,2∠ENM+∠ANE′=180°,
∴∠BM E′=180°﹣2∠EMN,∠ANE′=180°﹣2∠ENM,
∴∠BM E′+∠ANE′=360°﹣2(∠EMN+∠ENM),
∵∠EMN+∠ENM=180°﹣∠E,∠E=45°,
∴∠BM E′+∠ANE′=360°﹣2(∠EMN+∠ENM)
=360°﹣2(180°﹣∠E)
=2∠E
=90°.


科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;②AE=AF;③∠EBC=∠C;④FG∥AC;⑤EF=FG.其中正确的结论是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
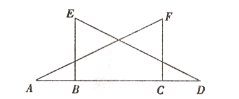
【题目】如图,△ACF≌△DBE,其中点A、B、C、D在一条直线上.
(1)若BE⊥AD,∠F=62°,求∠A的大小.
(2)若AD=9cm,BC=5cm,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:

∵DE∥BC(已知)
∴∠ADE= ( )
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=![]() ( )
( )
∠ABE=![]() ( )
( )
∴∠ADF=∠ABE
∴ ∥ ( )
∴∠FDE=∠DEB.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一张三角形纸片ABC,∠A=80°,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两张纸片均为等腰三角形,则∠C的度数可以是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需要粉刷一些相同的房间,经调查3名师傅一天粉刷8个房间,还剩40m2刷不完;5名徒弟一天可以粉刷9个房间;每名师傅比徒弟一天多刷30m2的墙面。
(1)求每个房间需要粉刷的面积;
(2)该公司现有36个这样的房间需要粉刷,若只聘请1名师傅和2名徒弟一起粉刷,需要几天完成?
(3)若来该公司应聘的有3名师傅和10名徒弟,每名师傅和每名徒弟每天的工资分别是240元和200元,该公司要求这36个房间要在2天内粉刷完成,问人工费最低是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满,根据下表提供的信息,解答以下问题
土特产种类 | 甲 | 乙 | 丙 |
每辆汽车运载量(吨) | 8 | 6 | 5 |
每吨土特产获利(百元) | 12 | 16 | 10 |
(1)设装运甲种土特产的车辆数为x,装运乙种土特产的车辆数为y,求y与x之间的函数关系式;
(2)如果装运每种土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).
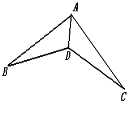
A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com