
【题目】某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满,根据下表提供的信息,解答以下问题
土特产种类 | 甲 | 乙 | 丙 |
每辆汽车运载量(吨) | 8 | 6 | 5 |
每吨土特产获利(百元) | 12 | 16 | 10 |
(1)设装运甲种土特产的车辆数为x,装运乙种土特产的车辆数为y,求y与x之间的函数关系式;
(2)如果装运每种土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值
【答案】(1)y=20―3x;
(2)三种方案,即:
方案一:甲种3辆 乙种11辆 丙种6辆
方案二:甲种4辆 乙种8辆 丙种8辆
方案三:甲种5辆 乙种5辆 丙种10辆
(3)方案一,即甲种3辆,乙种11辆,丙种6辆,最大利润为16.44万元
【解析】
试题(1)根据装运甲种土特产的车辆数为x,装运乙种土特产的车辆数为y,则装运丙种土特产的车辆数为20-x-y,结合表格数据,可得y与x之间的函数关系式;
(2)根据(1)中的函数及装运每种土特产的车辆都不少于3辆,可得车辆的安排方案;
(3)根据表格写出利润函数,结合(2)中的方案,即可求得最大利润的值.
(1)8x+6y+5(20―x―y)=120
∴y=20―3x
∴y与x之间的函数关系式为y=20―3x;
(2)由x≥3,y=20-3x≥3, 20―x―(20―3x)≥3可得![]()
又∵x为正整数
∴x=3,4,5
故车辆的安排有三种方案,即:
方案一:甲种3辆 乙种11辆 丙种6辆
方案二:甲种4辆 乙种8辆 丙种8辆
方案三:甲种5辆 乙种5辆 丙种10辆
(3)设此次销售利润为W元,
W=8x·12+6(20-3x)·16+5[20-x-(20-3x)]·10=-92x+1920
∵W随x的增大而减小 又x=3,4,5
∴ 当x=3时,W最大=1644(百元)=16.44万元
答:要使此次销售获利最大,应采用(2)中方案一,即甲种3辆,乙种11辆,丙种6辆,最大利润为16.44万元


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2,BC=4,P为矩形边上的一个动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以A,P,B为顶点的三角形面积为y,则选项图象能大致反映y与x的函数关系的是( )
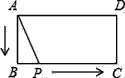
A. 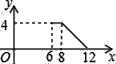 B.
B. 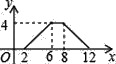 C.
C. 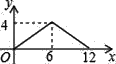 D.
D. 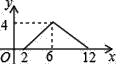
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,P是AD上一动点,O为BD的中点,连接PO并延长,交BC于点Q.
(1) 求证:四边形PBQD是平行四边形
(2) 若AD=6cm,AB=4cm, 点P从点A出发,以1cm/s的速度向点D运动(不与点D重合),设点P运动时间为t s , 请用含t的代数式表示PD的长,并求出当t为何值时,四边形PBQD是菱形。并求出此时菱形的周长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d,点A到图形G上各个点的距离的最大值称为该点到这个图形的最大距离D,定义点A到图形G的距离跨度为R=D﹣d. 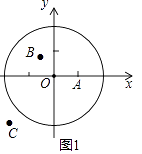
(1)①如图1,在平面直角坐标系xOy中,图形G1为以O为圆心,2为半径的圆,直接写出以下各点到图形G1的距离跨度: A(1,0)的距离跨度;
B(﹣ ![]() ,
, ![]() )的距离跨度;
)的距离跨度;
C(﹣3,﹣2)的距离跨度;
②根据①中的结果,猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是 .
(2)如图2,在平面直角坐标系xOy中,图形G2为以D(﹣1,0)为圆心,2为半径的圆,直线y=k(x﹣1)上存在到G2的距离跨度为2的点,求k的取值范围. 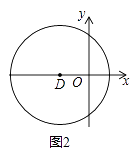
(3)如图3,在平面直角坐标系xOy中,射线OP:y= ![]() x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,直接写出圆心E的横坐标xE的取值范围 .
x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,直接写出圆心E的横坐标xE的取值范围 . 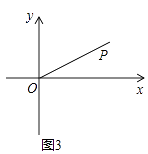
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:![]() ,过点M(1,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点M5的坐标为_____.
,过点M(1,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点M5的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在长方形ABCD中,AB=10cm,BC=8cm、点P从A出发,沿A、B、C、D路线运动,到D停止;点P的速度为每秒1cm,a秒时点P的速度变为每秒bcm,图②是点P出发x秒后,△APD的面积S1(cm2)与x(秒)的函数关系图象;
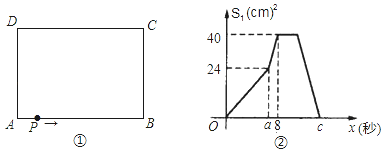
(1)根据图②中提供的信息,求a、b及图②中c的值;
(2)设点P离开点A的路程为y(cm),请写出动点P改变速度后y与出发后的运动时间x(秒)的函数关系式;
(3)点P出发后几秒,△APD的面积S1是长方形ABCD面积的![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解家长关注孩子成长方面的状况,学校开展了针对学生家长的“您最关心孩子哪方面成长”的主题调查,调查设置了“健康安全”、“日常学习”、“习惯养成”、“情感品质”四个项目,并随机抽取甲、乙两班共100位学生家长进行调查,根据调查结果,绘制了如图不完整的条形统计图. 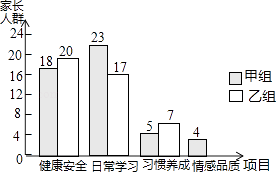
(1)补全条形统计图.
(2)若全校共有3600位学生家长,据此估计,有多少位家长最关心孩子“情感品质”方面的成长?
(3)综合以上主题调查结果,结合自身现状,你更希望得到以上四个项目中哪方面的关注和指导?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列叙述中正确的是( )
A. 直角三角形中,两条边的平方和等于第三边的平方
B. 若三角形三个内角度数之比为3:4:5,则该三角形是直角三角形
C. 在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,若![]() ,则∠B=90°
,则∠B=90°
D. △ABC的三边为a、b、c,且满足![]()
![]() ,则△ABC是直角三角形
,则△ABC是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长分别为2和4的两个全等三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止,设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )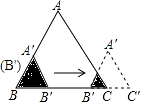
A.
B.
C.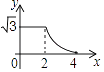
D.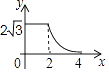
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com