
【题目】完成下面推理过程:
如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:

∵DE∥BC(已知)
∴∠ADE= ( )
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=![]() ( )
( )
∠ABE=![]() ( )
( )
∴∠ADF=∠ABE
∴ ∥ ( )
∴∠FDE=∠DEB.( )
【答案】∠ABC,两直线平行,同位角相等;∠ADE,∠ABC,角平分线的定义;DF,BE,同位角相等,两直线平行;两直线平行,内错角相等
【解析】
根据平行线的性质由DE∥BC得∠ADE=∠ABC,再根据角平分线的定义得到∠ADF=![]() ∠ADE,∠ABE=
∠ADE,∠ABE=![]() ∠ABC,则∠ADF=∠ABE,然后根据平行线的判定得到
∠ABC,则∠ADF=∠ABE,然后根据平行线的判定得到
DF∥BE,最后利用平行线的性质得∠FDE=∠DEB.
∵DE∥BC,
∴∠ADE=∠ABC,
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=![]() ∠ADE,
∠ADE,
∠ABE=![]() ∠ABC,
∠ABC,
∴∠ADF=∠ABE,
∴DF∥BE,
∴∠FDE=∠DEB.
故答案为∠ABC,两直线平行,同位角相等;∠ADE,∠ABC,角平分线的定义;DF,BE,同位角相等,两直线平行;两直线平行,内错角相等.


科目:初中数学 来源: 题型:
【题目】如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD(请填空)

解:∵EF∥AD
∴∠2= (
又∵∠1=∠2
∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=70°( )
∴∠AGD= ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ΔABC中,∠ABC的平分线与∠ACB的外角∠ACE的平分线相交于点D。

⑴.若∠ABC=60°,∠ACB=40°,求∠A和∠D的度数。
⑵.由⑴小题的计算结果,猜想,∠A和∠D有什么数量关系,并加以证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
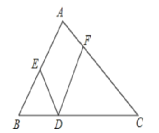
【题目】如图所示,在△ABC中,点D. E. F分别在BC、AB、AC上,且BD=BE,CD=CF,∠EDF=50°.则∠A的度数为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,已知∠AOB和C、D两点,用直尺和圆规作一点P,使PC=PD,且P到OA、OB两边距离相等.
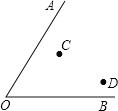
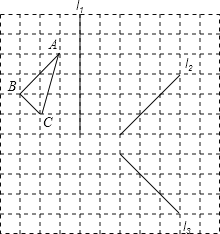
(2)用三角尺作图在如图的方格纸中,
①作△ABC关于直线l1对称的△A1B1C1;再作△A1B1C1关于直线l2对称的△A2B2C2;再作△△A2B2C2关于直线l3对称的△A3B3C3.
②△ABC与△A3B3C3成轴对称吗?如果成,请画出对称轴;如果不成,把△A3B3C3怎样平移可以与△ABC成轴对称?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MON=90°,点A,B分别在射线OM,ON上运动(不与点O重合),
观察:
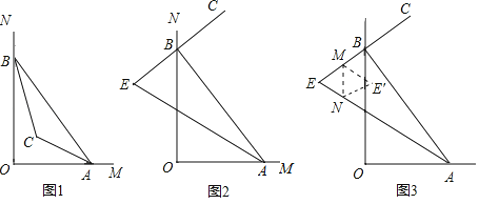
(1)如图1,若∠OBA和∠OAB的平分线交于点C,∠ACB= °
猜想:
(2)如图2,随着点A,B分别在射线OM,ON上运动(不与点O重合).若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点E,∠E的大小会变吗?如果不会,求∠E的度数;如果会改变,说明理由.
拓展:
(3)如图3,在(2)基础上,小明将△ABE沿MN折叠,使点E落在四边形ABMN内点E′的位置.求∠BME′+∠ANE′的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列有四个结论,其中正确的是( )
①若x 1![]() 1,则 x 只能是 2;
1,则 x 只能是 2;
②若x 1x![]() ax 1的运算结果中不含 x
ax 1的运算结果中不含 x![]() 项,则 a=1;
项,则 a=1;
③若2x 4 ![]() - 2x - 3
- 2x - 3![]() 有意义,则 x 的取值范围是 x 2 ;
有意义,则 x 的取值范围是 x 2 ;
④若 4![]() a,8
a,8![]() b,则2
b,则2![]() 可表示为
可表示为![]()
A.②④B. ②③④C. ①③④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列段文字,再解答问题:
已知在平面内有两点![]() 其两点间的距离公式为:
其两点间的距离公式为:
![]()
(1)已知点P(2,4)、Q(-3,-8),试求P、Q两点间的距离;
(2)已知点A(0,6)、B(-3,2)、C(3,2),判断线段AB、BC、AC中哪两条线段是相等的?并说明理由;
(3)已知点![]() 且MN=10,求
且MN=10,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l为正比例函数y=x的图象,点A1的坐标为(1,0),过点A1作x轴的垂线交直线l于点D1,以A1D1为边作正方形A1B1C1D1;过点C1作直线l的垂线,垂足为A2,交x轴于点B2,以A2B2为边作正方形A2B2C2D2;过点C2作x轴的垂线,垂足为A3,交直线l于点D3,以A3D3为边作正方形A3B3C3D3,…,按此规律操作下所得到的正方形AnBnCnDn的面积是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com