
【题目】在ΔABC中,∠ABC的平分线与∠ACB的外角∠ACE的平分线相交于点D。

⑴.若∠ABC=60°,∠ACB=40°,求∠A和∠D的度数。
⑵.由⑴小题的计算结果,猜想,∠A和∠D有什么数量关系,并加以证明。
【答案】(1)∠A=80°,∠D=40°;(2)∠A=2∠D,理由见解析
【解析】
(1)根据三角形内角和定理,已知∠ABC=60°,∠ACB=40°,易求∠A,根据角平分线定义和外角的性质即可求得∠D度数.
(2)根据三角形内角和定理以及角平分线性质,先求出∠D的等式,再与∠A比较即可解答.
(1)在△ABC中,∠ABC=60°,∠ACB=40°,
∴∠A=180°∠ABC∠ACB=80°,
∵BD为∠ABC,CD为∠ACE的角平分线,
∴∠DBC=![]() ∠ABC=
∠ABC=![]() ×60°=30°,
×60°=30°,
∠ACD=![]() (180°∠ACB)=
(180°∠ACB)=![]() ×140°=70°,
×140°=70°,
∴∠D=180°∠DBC∠ACB∠ACD=180°30°40°70°=40°,
∴∠A=80°,∠D=40°;
(2)通过第(1)的计算,得到∠A=2∠D,理由如下:
∵∠ACE=∠A+∠ABC,
∴∠ACD+∠ECD=∠A+∠ABD+∠DBE,∠DCE=∠D+∠DBC,
又∵BD平分∠ABC,CD平分∠ACE,
∴∠ABD=∠DBE,∠ACD=∠ECD,
∴∠A=2(∠DCE∠DBC),∠D=∠DCE∠DBC,
∴∠A=2∠D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】点C是直线l1上一点,在同一平面内,把一个等腰直角三角板ABC任意摆放,其中直角顶点C与点C重合,过点A作直线l2⊥l1,垂足为点M,过点B作l3⊥l1,垂足为点N

(1)当直线l2,l3位于点C的异侧时,如图1,线段BN,AM与MN之间的数量关系 (不必说明理由);
(2)当直线l2,l3位于点C的右侧时,如图2,判断线段BN,AM与MN之间的数量关系,并说明理由;
(3)当直线l2,l3位于点C的左侧时,如图3,请你补全图形,并直接写出线段BN,AM与MN之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-2x)(x2-2x+2)+1进行因式分解的过程:
解:设x2-2x=y
原式=y (y+2)+1 (第一步)
=y2+2y+1 (第二步)
=(y+1)2 (第三步)
=(x2-2x+1)2 (第四步)
请问:
(1)该同学因式分解的结果是否彻底? (填“彻底”或“不彻底”),若不彻底,则该因式分解的最终结果为 ;
(2)请你模仿上述方法,对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
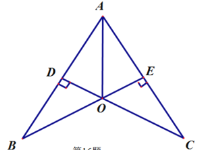
【题目】如图,已知CD⊥AB于点D,BE⊥ AC于点E, CD、 BE交于点O,且AO平分∠BAC,则图中的全等三角形共有_________________对。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;②AE=AF;③∠EBC=∠C;④FG∥AC;⑤EF=FG.其中正确的结论是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从超市出发,向东走了 3 千米到达小彬家,继续走 2.5 米到达小颖家,然后向西走了 10 千米到达小明家,最后回 到超市.
(1)小明家距小彬家多远?
(2)货车一共行驶了多少千米?
(3)货车每千米耗油 0.2 升,这次共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:

∵DE∥BC(已知)
∴∠ADE= ( )
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=![]() ( )
( )
∠ABE=![]() ( )
( )
∴∠ADF=∠ABE
∴ ∥ ( )
∴∠FDE=∠DEB.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
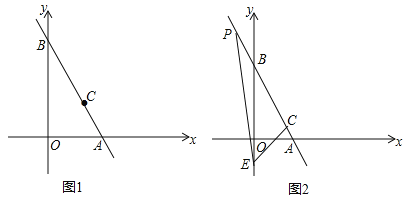
【题目】如图1,在平面直角坐标系中,直线AB经过点C(a,a),且交x轴于点A(m,0),交y轴于点B(0,n),且m,n满足![]() +(n﹣12)2=0.
+(n﹣12)2=0.
(1)求直线AB的解析式及C点坐标;
(2)过点C作CD⊥AB交x轴于点D,请在图1中画出图形,并求D点的坐标;
(3)如图2,点E(0,﹣2),点P为射线AB上一点,且∠CEP=45°,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com