
【题目】点C是直线l1上一点,在同一平面内,把一个等腰直角三角板ABC任意摆放,其中直角顶点C与点C重合,过点A作直线l2⊥l1,垂足为点M,过点B作l3⊥l1,垂足为点N

(1)当直线l2,l3位于点C的异侧时,如图1,线段BN,AM与MN之间的数量关系 (不必说明理由);
(2)当直线l2,l3位于点C的右侧时,如图2,判断线段BN,AM与MN之间的数量关系,并说明理由;
(3)当直线l2,l3位于点C的左侧时,如图3,请你补全图形,并直接写出线段BN,AM与MN之间的数量关系.
【答案】(1)MN=AM+BN;(2)MN=BN-AM,见解析;(3)见解析,MN=AM﹣BN.
【解析】
(1)利用AAS定理证明△NBC≌△MCA,根据全等三角形的性质、结合图形解答;
(2)根据直角三角形的性质得到∠CAM=∠BCN,证明△NBC≌△MCA,根据全等三角形的性质、结合图形解答;
(3)根据题意画出图形,仿照(2)的作法证明.
(1)MN=AM+BN
(2)MN=BN-AM
理由如下:如图2.
因为l2⊥l1,l3⊥l1
所以∠BNC=∠CMA=90°
所以∠ACM+∠CAM=90°
因为∠ACB=90°
所以∠ACM+∠BCN=90°
所以∠CAM=∠BCN
又因为CA=CB
所以△CBN≌△ACM(AAS)
所以BN=CM,NC=AM
所以MN=CM﹣CN=BN﹣AM
(3)补全图形,如图3
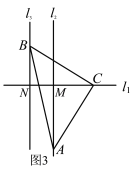
结论:MN=AM﹣BN
由(2)得,△CBN≌△ACM(AAS).
∴BN=CM,NC=AM
结论:MN=CN-CM=AM-BN.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知双曲线y1=![]() 与直线y2=ax+b交于点A(﹣4,1)和点B(m,﹣4).
与直线y2=ax+b交于点A(﹣4,1)和点B(m,﹣4).
(1)求双曲线和直线的解析式;
(2)直接写出线段AB的长和y1>y2时x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8…顶点依次用A1,A2,A3,A4,…表示,则顶点A2019的坐标是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为x千克,烤制时间为t,估计当x=2.8千克时,t的值为( )
A. 128B. 132C. 136D. 140
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用热气球探测器测量大楼AB的高度.从热气球P处测得大楼顶部B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离地面的高度为120m.试求大楼AB的高度(精确到0.1m).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校运动会需购买A、B两种奖品共100件![]() 、B两种奖品单价分别为10元、15元
、B两种奖品单价分别为10元、15元![]() 设购买A种奖品m件,购买两种奖品的总费用为W元.
设购买A种奖品m件,购买两种奖品的总费用为W元.
![]() 写出
写出![]() 元
元![]() 与
与![]() 件
件![]() 之间的函数关系式;
之间的函数关系式;
![]() 若购买两种奖品的总费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,求出自变量m的取值范围,并确定最少费用W的值.
若购买两种奖品的总费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,求出自变量m的取值范围,并确定最少费用W的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为6cm的⊙O中,点A是劣弧BC的中点,点D是优弧BC上一点,且∠D=30°,下列四个结论:①OA⊥BC;②BC=6![]() cm;③sin∠AOB=
cm;③sin∠AOB=![]() ;④四边形ABOC是菱形.其中正确结论的序号是( )
;④四边形ABOC是菱形.其中正确结论的序号是( )
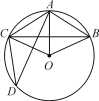
A. ①③ B. ①②③④ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD(请填空)

解:∵EF∥AD
∴∠2= (
又∵∠1=∠2
∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=70°( )
∴∠AGD= ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ΔABC中,∠ABC的平分线与∠ACB的外角∠ACE的平分线相交于点D。

⑴.若∠ABC=60°,∠ACB=40°,求∠A和∠D的度数。
⑵.由⑴小题的计算结果,猜想,∠A和∠D有什么数量关系,并加以证明。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com