
【题目】如图,利用热气球探测器测量大楼AB的高度.从热气球P处测得大楼顶部B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离地面的高度为120m.试求大楼AB的高度(精确到0.1m).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
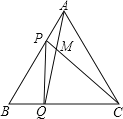
【题目】点P、Q分别是边长为4cm的等边![]() 的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是
的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是![]() ,设运动时间为t秒.
,设运动时间为t秒.
![]() 连接AQ、CP交于点M,则在P、Q运动的过程中,
连接AQ、CP交于点M,则在P、Q运动的过程中,![]() 变化吗:若变化,则说明理由,若不变,则求出它的度数;
变化吗:若变化,则说明理由,若不变,则求出它的度数;
![]() 连接PQ,
连接PQ,
![]() 当
当![]() 秒时,判断
秒时,判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 当
当![]() 时,则
时,则![]() ______秒
______秒![]() 直接写出结果
直接写出结果![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老张装修完新房,元旦期间到商场购买冰箱、电视机和洗衣机三件家电,刚好该商场推出新年优惠活动,具体优惠情况如下表:
购物金额(原价) | 折扣优惠 |
不超过3000元的部分 | 无折扣优惠 |
超过3000元但不超过10000元部分 | 九五折( |
超过10000元的部分 | 九折 |
付款时,还可以享受单笔消费满2000元立减160元优惠 | |
如:买原价5000元的商品,实际花费:
![]() (元)
(元)
(1)已知老张购买的这三件家电原价合计为11500元,如果一次性支付,请求出他的实际花费;
(2)如果在该商场购买一件原价为![]() 元的商品(
元的商品(![]() ).请用含
).请用含![]() 的代数式表示实际花费;
的代数式表示实际花费;
(3)付款前,老张突然想到:如果一次性支付,虽然折扣优惠更大,却只能享受一次立减160元优惠,如果将这三件家电分开支付或者两件合并支付.另一件单独支付,就可以享受多次立减160元优惠,已知老张购买的冰箱原价4800元,电视机原价4600元,洗衣机原价2100元,请你通过计算帮老张设计出最优惠的支付方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
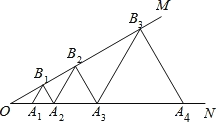
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△AnBnAn+1的边长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )

A. 105° B. 110° C. 100° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点C是直线l1上一点,在同一平面内,把一个等腰直角三角板ABC任意摆放,其中直角顶点C与点C重合,过点A作直线l2⊥l1,垂足为点M,过点B作l3⊥l1,垂足为点N

(1)当直线l2,l3位于点C的异侧时,如图1,线段BN,AM与MN之间的数量关系 (不必说明理由);
(2)当直线l2,l3位于点C的右侧时,如图2,判断线段BN,AM与MN之间的数量关系,并说明理由;
(3)当直线l2,l3位于点C的左侧时,如图3,请你补全图形,并直接写出线段BN,AM与MN之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系 ;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
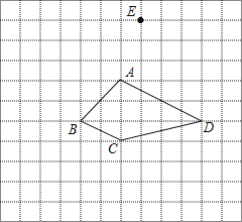
【题目】如图,方格纸中每个小方格都是边长为1的正方形,四边形ABCD的顶点与点E都是格点.
(1)作出四边形ABCD关于直线AC对称的四边形AB′CD′;
(2)求四边形ABCD的面积;
(3)若在直线AC上有一点P,使得P到D、E的距离之和最小,请作出点P(请保留作图痕迹),且求出PC=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
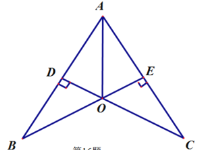
【题目】如图,已知CD⊥AB于点D,BE⊥ AC于点E, CD、 BE交于点O,且AO平分∠BAC,则图中的全等三角形共有_________________对。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com