
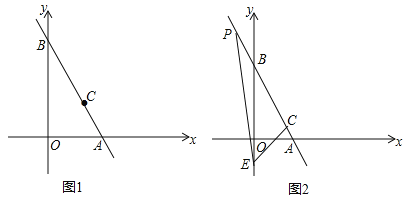
【题目】如图1,在平面直角坐标系中,直线AB经过点C(a,a),且交x轴于点A(m,0),交y轴于点B(0,n),且m,n满足![]() +(n﹣12)2=0.
+(n﹣12)2=0.
(1)求直线AB的解析式及C点坐标;
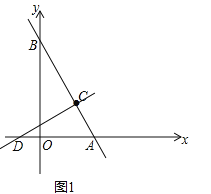
(2)过点C作CD⊥AB交x轴于点D,请在图1中画出图形,并求D点的坐标;
(3)如图2,点E(0,﹣2),点P为射线AB上一点,且∠CEP=45°,求点P的坐标.
【答案】(1)y=-2x+12,点C坐标(4,4);(2)画图形见解析,点D坐标(-4,0);(3)点P的坐标(![]() ,
,![]() )
)
【解析】
(1)由已知的等式可求得m、n的值,于是可得直线AB的函数解析式,把点C的坐标代入可求得a的值,由此即得答案;
(2)画出图象,由CD⊥AB知![]() 可设出直线CD的解析式,再把点C代入可得CD的解析式,进一步可求D点坐标;
可设出直线CD的解析式,再把点C代入可得CD的解析式,进一步可求D点坐标;
(3)如图2,取点F(-2,8),易证明CE⊥CF且CE=CF,于是得∠PEC=45°,进一步求出直线EF的解析式,再与直线AB联立求两直线的交点坐标,即为点P.
解:(1)∵![]() +(n﹣12)2=0,
+(n﹣12)2=0,
∴m=6,n=12,
∴A(6,0),B(0,12),
设直线AB解析式为y=kx+b,
则有![]() ,解得
,解得![]() ,
,
∴直线AB解析式为y=-2x+12,
∵直线AB过点C(a,a),
∴a=-2a+12,∴a=4,
∴点C坐标(4,4).
(2)过点C作CD⊥AB交x轴于点D,如图1所示,
设直线CD解析式为y=![]() x+b′,把点C(4,4)代入得到b′=2,
x+b′,把点C(4,4)代入得到b′=2,
∴直线CD解析式为y=![]() x+2,
x+2,
∴点D坐标(-4,0).
(3)如图2中,取点F(-2,8),作直线EF交直线AB于P,
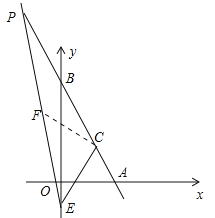
图2
∵直线EC解析式为y=![]() x-2,直线CF解析式为y=-
x-2,直线CF解析式为y=-![]() x+
x+![]() ,
,
∵![]() ×(-
×(-![]() )=-1,
)=-1,
∴直线CE⊥CF,
∵EC=2![]() ,CF=2
,CF=2![]() ,
,
∴EC=CF,
∴△FCE是等腰直角三角形,
∴∠FEC=45°,
∵直线FE解析式为y=-5x-2,
由![]() 解得
解得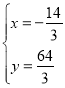 ,
,
∴点P的坐标为(![]() ).
).


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】在ΔABC中,∠ABC的平分线与∠ACB的外角∠ACE的平分线相交于点D。

⑴.若∠ABC=60°,∠ACB=40°,求∠A和∠D的度数。
⑵.由⑴小题的计算结果,猜想,∠A和∠D有什么数量关系,并加以证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列有四个结论,其中正确的是( )
①若x 1![]() 1,则 x 只能是 2;
1,则 x 只能是 2;
②若x 1x![]() ax 1的运算结果中不含 x
ax 1的运算结果中不含 x![]() 项,则 a=1;
项,则 a=1;
③若2x 4 ![]() - 2x - 3
- 2x - 3![]() 有意义,则 x 的取值范围是 x 2 ;
有意义,则 x 的取值范围是 x 2 ;
④若 4![]() a,8
a,8![]() b,则2
b,则2![]() 可表示为
可表示为![]()
A.②④B. ②③④C. ①③④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列段文字,再解答问题:
已知在平面内有两点![]() 其两点间的距离公式为:
其两点间的距离公式为:
![]()
(1)已知点P(2,4)、Q(-3,-8),试求P、Q两点间的距离;
(2)已知点A(0,6)、B(-3,2)、C(3,2),判断线段AB、BC、AC中哪两条线段是相等的?并说明理由;
(3)已知点![]() 且MN=10,求
且MN=10,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地有A,B,C三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时 公交车用时的频数 线路 |
|
|
|
| 合计 |
A | 59 | 151 | 166 | 124 | 500 |
B | 50 | 50 | 122 | 278 | 500 |
C | 45 | 265 | 167 | 23 | 500 |
早高峰期间,乘坐_________(填“A”,“B”或“C”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+4与x轴、y轴分别交于点A、B、C是线段AB上一点,四边形OADC是菱形,则OD的长为( )
x+4与x轴、y轴分别交于点A、B、C是线段AB上一点,四边形OADC是菱形,则OD的长为( )
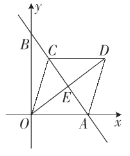
A. 4.2B. 4.8C. 5.4D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
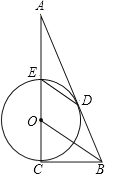
【题目】如图,CE是⊙O的直径,BC切⊙O于点C,连接OB,作ED∥OB交⊙O于点D,BD的延长线与CE的延长线交于点A.
(1)求证:AB是⊙O的切线;
(2)若⊙O的半径为1,tan∠DEO=![]() ,tan∠A=
,tan∠A=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l为正比例函数y=x的图象,点A1的坐标为(1,0),过点A1作x轴的垂线交直线l于点D1,以A1D1为边作正方形A1B1C1D1;过点C1作直线l的垂线,垂足为A2,交x轴于点B2,以A2B2为边作正方形A2B2C2D2;过点C2作x轴的垂线,垂足为A3,交直线l于点D3,以A3D3为边作正方形A3B3C3D3,…,按此规律操作下所得到的正方形AnBnCnDn的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,
(1)求证:AC=AE.
(2)若△BDE的周长是5cm,AB的长度为多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com